A. PHƯƠNG PHÁP GIẢI

1. Vẽ thêm đường trung bình để tính góc, tính độ dài đoạn thẳng

Vẽ thêm đường trung bình của một tam giác, của một hình thang bằng một trong ba cách vẽ sau: vẽ thêm trung điểm một đoạn thẳng, vẽ đường thẳng song song, vẽ đường thẳng vuông góc.

Sử dụng:

• Định lí đường trung bình của tam giác, của hình thang
• Tính chất về góc trong tam giác
• Tính chất hai góc ở vị trí so le hoặc đồng vị của hai đường thẳng song song.
• Trong một tam giác, đối diện với hai cạnh bằng nhau là hai góc bằng nhau và ngược lại.
• Tính chất góc ngoài của tam giác bằng tổng hai góc trong không kề với nó.

Ví dụ 1: Tính x, y trên hình.

Hướng dẫn:

Do IP, GK, MH cùng vuông góc với AH nên IP // GK // MH

Lại có AI = IG = GM

$\Rightarrow $ AP = PK = KH, do đó IP là đường trung bình của tam giác AGK; GK là đường trung bình của hình thang IPHM.

Áp dụng định lí đường trung bình vào tam giác AGK và hình thang IPHM ta được: GK = 2IP hay 6cm = 2x $\Leftrightarrow $ x = 3cm

GK = $\frac{IP+MH}{2}$ hay $6 = \frac{3+y}{2}\Leftrightarrow y=9$ (cm)

2. Vẽ thêm đường trung bình để chứng minh quan hệ về độ dài

Ta vẽ thêm đường trung bình. Sau đó áp dụng định lí đường trung bình của tam giác, của hình thang.

Ví dụ 2: Cho $\Delta $ABC có AM là đường trung tuyến. Gọi I là trung điểm của AM và D là giao điểm của CI và AB. Chứng minh rằng: DA = $\frac{1}{2}$DB; DI = $\frac{1}{4}$DC.

Hướng dẫn:

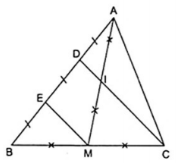
Do M là trung điểm của BC theo giả thiết nên vẽ thêm E là trung điểm của BD thì BE = ED (1)

Ta được EM là đường trung bình của $\Delta $BCD

Áp dụng định lí đường trung bình vào $\Delta $BCD, ta được:

ME // DC (2) và DC = 2ME (3)

Từ (2) $\Rightarrow $ ME // DI mà AI = IM theo giả thiết

Áp dụng định lí đường trung bình vào $\Delta $AME ta được AD = DE (4)

Từ (1) và (4) suy ra AD = DE = EB (5) hay AD = $\frac{1}{2}$DB

Từ (4) và (5) ta có DI là đường trung bình của $\Delta $AEM.

Áp dụng định lí đường trung bình vào $\Delta $AEM ta có ME = 2DI (6)

Thay (6) vào (3) ta được: DC = 2.2DI = 4DI hay DI = $\frac{1}{2}$DC

3. Vẽ thêm đường trung bình để chứng minh hai đường thẳng song song, chứng minh ba điểm thẳng hàng

Ta vẽ thêm đường trung bình

Áp dụng định lí đường trung bình của tam giác, của hình thang

Sử dụng tiên đề Ơ-clít về đường thẳng song song: Qua một điểm ở ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó hoặc sử dụng tính chất: Nếu một góc là góc bẹt thì hai cạnh của góc ấy là hai tia đối nhau hay hai cạnh của góc này nằm trên một đường thẳng.

Ví dụ 3: Cho $\Delta $ABC kéo dài trung tuyến BD đến F sao cho DF = BD và trung tuyến CE đến G sao cho EG = CE. Chứng minh ba điểm G, A, F thẳng hàng.

Hướng dẫn:

Vì BD, CE là hai trung tuyến của $\Delta $ABC theo giả thiết nên D, E lần lượt là trung điểm của AC, AB hay AD = DC, AE = EB. 

Từ giả thiết DF = BD, EG = CE suy ra ED là đường trung bình của hai tam giác ACG và ABF.

Áp dụng định lí đường trung bình vào hai tam giác trên, ta được:

GA // ED và AF // ED

$\Rightarrow $ G, A, F thẳng hàng (vì qua điểm A nằm ngoài đường thẳng ED chỉ có một đường thẳng song song với ED)