A. PHƯƠNG PHÁP GIẢI

1. Tính diện tích hình tứ giác có hai đường chéo vuông góc

Hình tứ giác ABCD có hai đường chéo AC, BD vuông góc, diện tích hình tứ giác được tính theo công thức:

S_ABCD = $\frac{1}{2}$AC.BD

Ví dụ 1: Tính diện tính hình thang cân ABCD (AB // CD) có AC vuông góc với BD và chiều cao h.

Hướng dẫn:

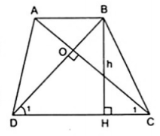
Từ giả thiết ABCD là hình thang cân nên AC = BD.

Áp dụng công thức tính diện tính hình từ giác có hai đường chéo vuông góc ta có:
S_ABCD = $\frac{1}{2}$BD.AC = $\frac{1}{2}BD^{2}$

Kẻ BH $\perp $ CD thì BH = h.

Ta có $\Delta $ACD = $\Delta $BDC (c.c.c) 

$\Rightarrow \widehat{D_{1}}=\widehat{C_{1}}$ nên $\Delta $OCD vuông cân ở O.

Do đó $\widehat{D_{1}}=45^{\circ}$ suy ra $\Delta $BHD vuông tại H, ta được:

$BH^{2}+DH^{2}=BD^{2}$ Hay $BD^{2}=h^{2}+h^{2}=2h^{2}$

Vậy $S_{ABCD}=\frac{1}{2}.2h^{2}=h^{2}$

2. Tính diện tích hình thoi

Ta sử dụng công thức tính diện tích hình tứ giác có hai đường chéo vuông góc hoặc công thức tính diện tích hình bình hành.
Ví dụ 2: Cho hình thoi ABCD có AB = 6cm, $\widehat{A}=60^{\circ}$. Tính diện tích hình thoi.

Hướng dẫn:

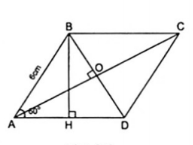
Theo công thức ta có diện tích hình thoi ABCD là:

$S_{ABCD}=\frac{1}{2}AC.BD$

Gọi O là giao điểm của AC và BD thì AC = 2AO; BD = 2BO nên $S_{ABCD}=2AO.BO$

Từ giả thiết có $\widehat{A}=60^{\circ}$ suy ra $\Delta $ABD là tam giác đều

$\Rightarrow \Delta $ABO vuông tại O có $\widehat{ABO}=60^{\circ}$ nên:

BO = $\frac{1}{2}$AB = 3 (cm)

AO = $\frac{\sqrt{3}}{2}$AB = 3$\sqrt{3}$ (cm)

$\Rightarrow S_{ABCD}=2.3\sqrt{3}.3=18\sqrt{3} (cm^{2})$