A. PHƯƠNG PHÁP GIẢI

1. Chứng minh ba điểm thẳng hàng

Ta chứng minh 3 điểm thẳng hàng nhờ :

• Tính chất góc bẹt.
• Tính chất về đường chéo hình chữ nhật.
• Tiên đề Ơ-clít về đường thẳng song song.

Ví dụ 1: Một đội công nhân đang trồng cây trên đoạn đường AB thì gặp chướng ngại vật che lấp tầm nhìn. Độ đã dựng các điểm C, D, E như trên hình vẽ rồi trồng cây tiếp trên đoạn đường EF vuông góc với DE. Vì sao AB và EF cùng nằm trên một đường thẳng.

Hướng dẫn:

Theo hình bên ta thấy, tứ giác BCDE có BC = ED và BC // ED vì có góc trong cùng phía bù nhau.

Do đó tứ giác BCDE là hình bình hành.

Tứ giác BCDE là hình bình hành có góc C vuông nên là hình chữ nhật.

Do đó $\widehat{CBE}=\widehat{DEB}=90^{\circ}\Rightarrow \widehat{ABE}=\widehat{BEF}=180^{\circ}$

$\Rightarrow $ A, B, E thẳng hàng và B, E, F thẳng hàng. Hay 4 điểm A, B, E, F thẳng hàng.

Vậy AB và EF cùng nằm trên một đường thẳng.

2. Vẽ thêm hình chữ nhật để tính độ dài đoạn thẳng, tính góc, chứng minh quan hệ về độ dài

- Ta vẽ thêm hình chữ nhật bằng cách kẻ đường vuông góc hoặc vẽ thêm hình bình hành có một góc vuông

- Sau đó ta áp dụng các tính chất:

Tính chất về cạnh hoặc đường chéo hình chữ nhật

Định lí Py-ta-go

Định lí đường trung tuyến với cạnh huyền của một tam giác vuông

Ví dụ 2: Tìm x trên hình vẽ dưới đây.

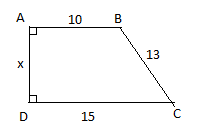
Hướng dẫn:

Kẻ BH $\perp $ DC thì tứ giác ABHD có ba góc vuông nên nó là hình chữ nhật.

Áp dụng tính chất về cạnh vào hình chữ nhật ABHD ta được:

• DH = AB = 10
• BH = AD = x

Do đó CH = CD - DH = 15 - 10 = 5

Áp dụng định lí Py-ta-go vào $\Delta $BHC vuông tại H ta được:

$BC^{2}=CH^{2}+HB^{2}\Rightarrow 13^{2}=5^{2}+x^{2}\Leftrightarrow x^{2}=144\Leftrightarrow x=12$

Vậy x = 12

3. Vẽ thêm đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh quan hệ về độ dài và tính góc

- Ta xác định tam giác vuông để vẽ thêm trung tuyến ứng với cạnh huyền

- Sau đó ta áp dụng tính chất về đường trung tuyến ứng với cạnh huyền hoặc dấu hiệu nhận biết tam giác vuông để giải bài toán.

Ví dụ 3: Cho hình thang cân ABCD có AB // CD; AB < CD. Đường cao AH. Gọi M, N lần lượt là trung điểm của AD và BC. Tính độ dài đoạn MN biết HC = 5cm.

Hướng dẫn:

Từ giả thiết ta có MN là đường trung bình của hình thang cân ABCD

Áp dụng định lí đường trung bình vào hình thang ABCD ta được:

MN // DC $\Rightarrow $ MN // HC

AH là đường cao của hình thang nên AH $\perp $ DC hay $\Delta $ADH vuông tại H.

Mà M là trung điểm của AD nên HM là đường trung tuyến ứng với cạnh huyền AD của $\Delta $AHD vuông.

$\Rightarrow $ HM = $\frac{1}{2}$AD và AM = MD

$\Rightarrow $ MH = MD

$\Rightarrow $ $\Delta $MDH cân tại M $\Rightarrow $ $\widehat{D}=\widehat{H_{1}}$

Lại có $\widehat{D}=\widehat{C}$ (do hình thang ABCD cân)

$\Rightarrow $ $\widehat{C}=\widehat{H_{1}}$. Do đó MH // NC

Xét tứ giác MHNC có ;

• MH // NC
• MN // HC

$\Rightarrow $ tứ giác MHNC là hình bình hành.

$\Rightarrow $ MN = HC = 5 (cm)