Bài tập về vẽ thêm đường trung tuyến ứng với cạnh huyền của tam giác vuông để chứng minh quan hệ về độ dài và tính góc

5.

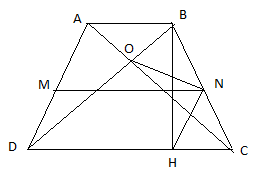
Gọi M, N là trung điểm của AD và BC thì MN là đường trung bình của hình thang ABCD.

Nối HN, $\Delta $BHC vuông tại H có N là trung điểm của BC nên HN = NC = $\frac{1}{2}$BC

Mà DM = $\frac{1}{2}$AD = \frac{1}{2}$BC

$\Rightarrow $ DM = HN (1)

$\Delta $HNC có HN = NC nên $\Delta $HNC cân tại N $\Rightarrow $ $\widehat{NHC}=\widehat{NCH}$

Mà $\widehat{NCH}=\widehat{MDH}$

$\Rightarrow $ $\widehat{NHC}=\widehat{MDH}$ $\Rightarrow $ DM // NH (2)

Từ (1) và (2) $\Rightarrow $ tứ giác DMNH là hình bình hành

$\Rightarrow $ MN = DH (3)

Vì hình thang ABCD cân nên $\widehat{ODC}=\widehat{OCD}$

Mà OD $\perp $ OC

$\Rightarrow \widehat{ODC}=45^{\circ}$ Hay $\widehat{BDH}=45^{\circ}$

$\Delta $BHD vuông tại H có $\widehat{BDH}=45^{\circ}$

$\Rightarrow $ $\Delta $BHD vuông cân tại H 

$\Rightarrow $ BH = DH (4)

Từ (3), (4) $\Rightarrow $ BH = MN (đ.p.c.m)

6.

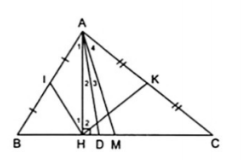
a) Áp dụng định lí trung tuyến ứng với cạnh huyền vào tam giác vuông ABC ta được:

MA = $\frac{1}{2}$BC; BM = MC

$\Rightarrow $ MA = MC nên $\widehat{A_{4}}=\widehat{C}$ 

Lại có $\widehat{A_{1}}=\widehat{C}$ do cùng phụ với $\widehat{B}$, suy ra $\widehat{A_{1}}=\widehat{A_{4}}$

Vậy $\widehat{HAB}=\widehat{MAC}$ (1)

b) Vì AD là phân giác của góc A theo giả thiết nên $\widehat{BAD}=\widehat{DAC}$ (2)

Từ (1), (2) $\Rightarrow \widehat{A_{2}}=\widehat{A_{3}}$

Do đó AD là tia phân giác của $\widehat{HAM}$

c) Chứng minh tương tự câu a) ta được $\widehat{H_{1}}=\widehat{A_{1}}$ (3) và $\widehat{H_{2}}=\widehat{HAC}$ (4)

Cộng từng vế (3) và (4) ta được: $\widehat{IHK}=\widehat{A}=90^{\circ}$

Vậy IH $\perp $ HK