A. PHƯƠNG PHÁP GIẢI

1. Vẽ thêm các đường thẳng song song cách đều để chứng minh quan hệ về độ dài

- Ta vẽ thêm đường thẳng song song hoặc đường vuông góc để tạo ra các đường thẳng song song cách đều.

- Áp dụng tính chất của các đường thẳng song song cách đều: 

• Những đường thẳng song song cách đều chắn trên một đường thẳng bất kì những đoạn thẳng liên tiếp bằng nhau.

Ví dụ 1: Cho $\Delta $ABC có D là trung điểm của AB. Kẻ DE // BC. (E $\in $ AC). Chứng minh rằng AE = EC.

Hướng dẫn:

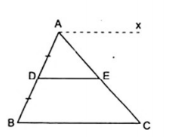
Do DE // BC theo giả thiết. Ta vẽ thêm Ax // DE thì Ax // DE // BC.

Vì D là trung điểm của AB nên AD = DB.

$\Rightarrow $ Ax, DE, BC là ba đường thẳng song song cách đều nên nó chắn trên đường thẳng AC hai đoạn thẳng bằng nhau liên tiếp là AE = EC.

2. Cho một điểm di chuyển trên một đường, tìm xem một điểm khác phụ thuộc vào điểm đó di chuyển trên đường thẳng song song nào

- Ta xác định điểm di chuyển

- Xác định điểm, đường thẳng hoặc tam giác cố định để tìm đoạn có độ dài không đổi

- Sử dụng tính chất của các điểm cách đều một đường htẳng cho trước.

Ví dụ 2: Cho điểm A ở ngoài đường thẳng d và có khoảng cách đến d bằng 2cm. Trên d lấy một điểm B bất kì. Gọi C là điểm đối xứng với điểm A qua điểm B. Hỏi khi điểm B di chuyển trên đường thẳng d thì điểm C di chuyển trên đường thẳng nào?

Hướng dẫn:

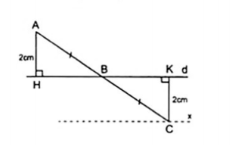
Kẻ AH $\perp $ d và CK $\perp $ d thì AH là khoảng cách từ điểm A cố định đến đường thẳng d cố định nên AH = 2cm không đổi.

CK là khoảng cách từ C đến đường thẳng d.

Khi B di chuyển trên d thì C cũng di chuyển theo

Áp dụng tính chất hai điểm đối xứng qua tâm và hai góc đối đỉnh ta được: 

$\widehat{H}=\widehat{K}=90^{\circ}$

AB = CB

$\widehat{B_{1}}=\widehat{B_{2}}$

$\Rightarrow \Delta $AHB = $\Delta $AKB (cạnh huyền - góc nhọn)

$\Rightarrow $ CK = AH = 2cm.

Như vậy điểm C cách đường thẳng d cố định một khoảng không đổi 2cm nên C di chuyển trên đường thẳng Cx // d và cách d một khoảng bằng 2cm.