A. PHƯƠNG PHÁP GIẢI

1. Chia đa thức cho đơn thức

Ta lấy từng hạng tử của đa thức chia cho đơn thức rồi cộng các kết quả lại.

Ví dụ 1: Thực hiện phép chia:

a) $(a^{3}-2a^{2}b+3ab^{2}):\frac{1}{2}a$

b) $[3(x-y)^{4}+2(x-y)^{3}-5(x-y)^{2}]:(x-y)^{2}$

Hướng dẫn:

a) $(a^{3}-2a^{2}b+3ab^{2}):\frac{1}{2}a$

 = $2a^{2}-4ab+6b^{2}$

b) $[3(x-y)^{4}+2(x-y)^{3}-5(x-y)^{2}]:(x-y)^{2}$

 = $3(x-y)^{2}+2(x-y)-5$

2. Chia đa thức đã sắp xếp

Sắp xếp các đa thức theo lũy thừa giảm dần của lũy thừa của biến

Đặt phép chia như phép chia các số

Lấy hạng tử cao nhất của đa thức bị chia chia cho hạng tử cao nhất của đa thức chia.

Lấy thương nhân với đa thức chia và đặt kết quả dưới dòng đa thức bị chia

Lấy hiệu của đa thức bị chia với tích vừa tìm được.

Tiếp tụ làm như vậy đến khi được dư bằng 0 hoặc dư là đa thức có bậc nhỏ hơn đa thức chia.

Ví dụ 2: Thực hiện các phép chia:

a) $(x^{2}-5x+4):(x-1)$

b) $(x^{3}+3x^{2}+3x+1):(x+1)$

c) $(x^{3}+6x^{2}+11x+6):(x^{2}+3x+2)$

d) $(x^{3}+3x^{2}-x-3):(x^{2}+2x-3)$

e) $(x^{2}+5x+6):(x-4)$

Hướng dẫn:

a) $(x^{2}-5x+4):(x-1)$

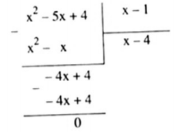
Vậy đa thức $(x^{2}-5x+4)$ chia hết cho (x-1) được thương là x-4

b) $(x^{3}+3x^{2}+3x+1):(x+1)$

Vậy đa thức $(x^{3}+3x^{2}+3x+1)$ chia hết cho (x+1) được thương là $(x^{2}+2x+1)$

c) $(x^{3}+6x^{2}+11x+6):(x^{2}+3x+2)$

Vậy đa thức $(x^{3}+6x^{2}+11x+6)$ chia hết cho $(x^{2}+3x+2)$ được thương là (x+3)

d) $(x^{3}+3x^{2}-x-3):(x^{2}+2x-3)$

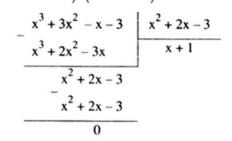
Vậy đa thức $(x^{3}+3x^{2}-x-3)$ chia hết cho $(x^{2}+2x-3)$ được thương là (x+1)

e) $(x^{2}+5x+6):(x-4)$

Vậy đa thức $(x^{2}+5x+6)$ chia cho (x-4) thì được (x+9) và dư bằng 42.