A. PHƯƠNG PHÁP GIẢI

1. Sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng

Ta sử dụng định nghĩa, tính chất và bổ đề về hình vuông.

Ví dụ 1: Cho hình vuông ABCD. Trên cạnh BC lấy điểm M, trên cạnh CD lấy điểm N sao cho BM = CN. Chứng minh rằng AM = BN và AM $\perp $ BN.

Hướng dẫn:

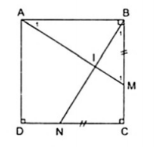
Áp dụng định nghĩa và giả thiết vào hình vuông ABCD ta được:

• AB = BC
• $\widehat{A}=\widehat{B}=90^{\circ}$
• BM = CN

$\Rightarrow $ $\Delta $ABM = $\Delta $BCN (c.g.c)

$\Rightarrow $ AM = BN

Gọi I là giao điểm của AM và BN

Áp dụng tính chất về góc vào tam giác vuông ABM và BCN kết quả của hai tam giác bằng nhau ta được:

$\widehat{A_{1}}+\widehat{M_{1}}=90^{\circ}$

$\widehat{B_{1}}=\widehat{A_{1}}$

$\Rightarrow $ $\widehat{B_{1}}+\widehat{M_{1}}=90^{\circ}$ (1)

Áp dụng tính chất về góc vào $\Delta $BIM ta có $\widehat{B_{1}}+\widehat{M_{1}}+\widehat{I_{1}}=180^{\circ}$ (2)

Từ (1) và (2) $\Rightarrow \widehat{I_{1}}=90^{\circ}$

Do đó AM $\perp $ BN

2. Tìm điều kiện để một hình trở thành hình vuông

- Ta sử dụng dấu hiệu nhận biết hình vuông.

- Nếu bài toán chỉ yêu cầu tìm vị trí của một điểm nào đó để một hình trở thành hình vuông ta làm như sau: Giả sử hình đó là hình vuông rồi dựa vào các tính chất của hình vuông để chỉ ra vị trí cần tìm.

Ví dụ 2: Cho $\Delta $ABC, D là điểm nằm giữa B và C. Qua D kẻ các đường thẳng song song với AB và AC, chúng cắt các cạnh AC và AB theo thứ tự ở E và F.

a) Tứ giác AEDF là hình gì? Vì sao?

b) Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDF là hình thoi?

c) Nếu tam giác ABC vuông tại A thì tứ giác AEDF là hình gì? Điểm D ở vị trí nào trên cạnh BC thì tứ giác AEDFD là hình vuông?

Hướng dẫn: 

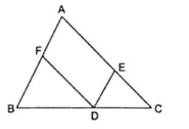
a) Tứ giác AEDF là hình bình hành

Từ giả thiết ta được : DE // AC và DF // AB

$\Rightarrow $ DE // AF và DF // AE

Tứ giác AEDF có các cạnh đối song song nên nó là hình bình hành

b) AEDF là hình thoi thì nó là hình bình hành và có AD là tia phân giác của $\widehat{FAE}$

Vậy AD là đường phân giác của $\widehat{BAC}$ thì tứ giác AEDF là hình thoi.

c) Nếu $\Delta $ABC vuông tại A thì hình bình hành AEDF là hình chữ nhật.

Để hình chữ nhật AEDF là hình vuông thì cần có AF = AE

$\Rightarrow \widehat{FAD}=\widehat{DAE}$. Hay AD là đường phân giác của $\widehat{BAC}$

Vậy D thuộc BC và AD là đường phân giác của $\widehat{BAC}$ thì tứ giác AEDF là hình vuông.