Bài tập về sử dụng định nghĩa, tính chất của hình vuông để chứng minh các quan hệ bằng nhau, song song, vuông góc, thẳng hàng

1.

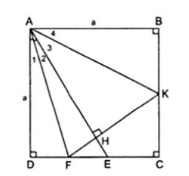
a) Xét $\Delta $ADF và $\Delta $AHF là 2 tam giác vuông có:

$\widehat{A_{1}}=\widehat{A_{2}}$

chung cạnh huyền AF

$\Rightarrow $ $\Delta $ADF = $\Delta $AHF (cạnh huyền - góc nhọn)

$\Rightarrow $ AH = AD = a

b) Xét $\Delta $AHK và $\Delta $ABK là hai tam giác vuông có:

chung cạnh huyền AK

AH = AB = a

$\Rightarrow $ $\Delta $AHK = $\Delta $ABK (cạnh huyền - cạnh góc vuông)

$\Rightarrow \widehat{A_{3}=\widehat{A_{4}}}$

Do đó ta được: $\widehat{FAK}=\widehat{A_{2}}+\widehat{A_{3}}=\frac{1}{2}\widehat{DAE}+\frac{1}{2}\widehat{EAB}=\frac{1}{2}\widehat{BAC}=45^{\circ}$

2. 

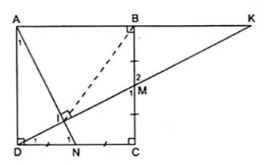
a) Áp dụng định nghĩa và giả thiết vào hình vuông ABCD ta được :

AD = DC, $\widehat{D}=\widehat{C}=90^{\circ}$

DN = CM

$\Rightarrow $ $\Delta $ADN = $\Delta $DCM (2 cạnh góc vuông)

$\Rightarrow \widehat{A_{1}}=\widehat{D_{1}}$

Vì $\Delta $ADN vuông ở D nên $\widehat{A_{1}}+\widehat{N_{1}}=90^{\circ}$

$\Rightarrow \widehat{D{1}}+\widehat{N_{1}}=90^{\circ}$

$\Rightarrow \Delta $DIN vuôn ở I.

Vậy AN $\perp $ DM.

b) Gọi giao điểm của DM với AB là K. Khi đó

$\Delta $DMC = $\Delta $KMB (cạnh góc vuông - góc nhọn kể)

$\Rightarrow $ DC = BK

Mà AB = DC nên AB = BK

$\Rightarrow $ IB là trung tuyến ứng với cạnh huyền của $\Delta $AIK vuông. Do đó IB = AB

3. 

Xét hình vuông ABCD có AB = BC = 1m

Ta đi dựng hình vuông nhận đường chéo AC làm cạnh đề tính đường chéo của hình vuông mới này.

Trên tia đối của tia BA lấy điểm E, tia đối của tia BC lấy điểm F sao cho BE = BF = 1m. 

Ta được tứ giác AFEC có hai đường chéo bằng nhau, vuông góc với nhau và cắt nhau tại trung điểm của mỗi đường nên nó là hình vuông cạnh AC.

Hình vuông này có đường cheo AE = 2m

4. 

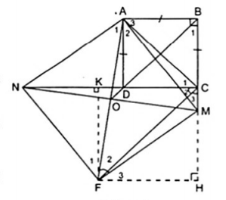
a) $\Delta $ABM = $\Delta $ADN (c.g.c)

$\Rightarrow $ AM = AN; $\widehat{A_{1}}=\widehat{A_{3}}$

Hình bình hành MANF có hai cạnh kề bằng nhau nên là hình thoi.

 Do $\widehat{A_{2}}$ phụ với $\widehat{A_{3}}$ nên $\widehat{A_{1}}$ phụ với $\widehat{A_{2}}$. Hay $\widehat{MAN}=90^{\circ}$

Điều này chứng tỏ hình thoi MANF là hình vuông vì có một góc vuông.

b) Kẻ FH, FK theo thứ tự vuông góc với hai đường thẳng BC, NC. Ta được tứ giác KCHF có ba góc vuông nên là hình chữ nhật

$\Rightarrow \widehat{KFH}=90^{\circ}$

Lại có $\widehat{NFM}=90^{\circ}$ vì là góc của hình vuông nên $\widehat{F_{1}}=\widehat{F_{3}}$ do cùng phụ với $\widehat{F_{2}}$.

Từ đó ta được $\Delta $FKN = $\Delta $FHM (cạnh huyền - góc nhọn)

$\Rightarrow $ FH = FK.

Điều này chứng tỏ điểm F cách đều hai cạnh CM, CN của $\widehat{MCN}$ nên F thuộc tia phân giác của $\widehat{MCN}$

c) Theo tính chất về đường chéo của hình vuông và từ câu b) ta có: $\widehat{C_{1}}=\widehat{C_{2}}=45^{\circ}\Rightarrow \widehat{ACF}=90^{\circ}\Rightarrow AC\perp CF$

d) Tương tự như trên ta có $\widehat{B_{1}}=\widehat{C_{3}}=45^{\circ}$

$\Rightarrow $ OB // CF

Tứ giác BOFC có hai cạnh đối song song nên là hình thang.