A. PHƯƠNG PHÁP GIẢI

Chứng minh quan hệ về độ dài, ta sử dụng:

Tính chất về cạnh bên và đường chéo của hình thang cân.

Trong một tam giác, đối diện với hai góc bằng nhau là hai cạnh bằng nhau và ngược lại.

Tính độ dài đoạn thẳng:

Chọn tam giác vuông thích hợp chứa đoạn thẳng rồi áp dụng định lí Py-ta-go.

Ví dụ 1: Cho hình thang cân ABCD có AB // CD, AB < CD. Kẻ các đường cao AH, BK của hình thang. Chứng minh rằng DH = CK.

Hướng dẫn:

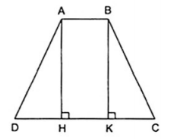
Áp dụng định nghĩa, tính chất và giải thiết vào hình thang cân ABCD ta được:

• $\widehat{D}=\widehat{C}$
• AD = BC
• $\widehat{H}=\widehat{K}=90^{\circ}$

$\Rightarrow \Delta $ADH = $\Delta $BCK (trường hợp cạnh huyền - góc nhọn)

$\Rightarrow $ DH = CK

Ví dụ 2: Tính chiều cao của hình thang cân ABCD, biết rằng cạnh bên AD = 5cm, các cạnh đáy AB = 6cm và CD = 14cm.

Hướng dẫn:

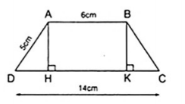
Kẻ $AH\perp DC;BK\perp DC$ thì AH // BK nên hình thang ABKH có hai cạnh bên song song.

$\Rightarrow $ AH = BK, HK = AB = 6cm

Áp dụng định lí Py-ta-go vào $\Delta $ADH vuông tại H ta được:

$AD^{2}=DH^{2}+HA^{2}$ hay $5^{2}=4^{2}+HA^{2}$

$\Leftrightarrow HA^{2}=9\Leftrightarrow HA=3$(cm)

Vậy chiều cao của hình thang cân là 3cm.