Bài tập về vẽ thêm các đường thẳng song song cách đều để chứng minh quan hệ về độ dài

1.

Từ giả thiết ta có BH // MI // CK (vì cùng vuông góc với AD) và BM = MC.

Do đó BH, MI, CK là ba đường thẳng song song cách đều nhau.

Do đó chúng chắn trên đường thẳng AD hai đoạn thẳng liên tiếp bằng nhau là HI = IK.

2.

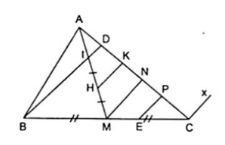
Gọi H, E thứ tự là trung điểm của IM và MC. Kết hợp với giả thiết AM = 3AI ta có AI = IH = HM.

Qua H, M, E lần lượt kẻ HK, MN, EP cùng song song với ID.

Ta được MN là đường trung bình của $\Delta $BDC nên DN = NC.

Từ đó ta thu được bốn đường thẳng song song cách đều là ID, HK, MN, EP nên chúng chắn trên AC năm đoạn thẳng liên tiếp bằng nhau là :

AD = DK = KN = NP = PC

Do đó AD = $\frac{1}{5}$AC

3.

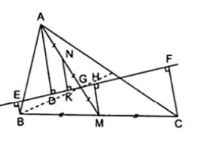
Gọi N là trung điểm của AG và M là giao điểm của AG với BC thì BM = MC và K, H thứ tự là chân đường vuông góc kẻ từ N, M đến đường thẳng d. Kết hợp với giả thiết ta có:

AD // NK // MH // BE // CF

a) 

Ta có BE, MH, CF là ba đường thẳng song song cách đều nên chúng chắn trên d hai đoạn thẳng liên tiếp bằng nhau là EG = GF. Do đó MH là đường trung bình của hình thang BEF, suy ra

BE + CF = 2HM (1), theo định lí đường trung bình.

Mặt khác AD, NK, MH cũng là ba đường thẳng song song cách đều nên chúng chắn trên d ba đoạn thẳng liên tiếp bằng nhau là DK = KG = GH.

Do đó NK là đường trung bình của $\Delta $AGD và $\Delta $NKG = $\Delta $MHG (c.g.c)

$\Rightarrow $ AD = 2NK = 2MH

Thay 2MH = AD vào đẳng thức (1) ta được BE + CF = AD.

b) 

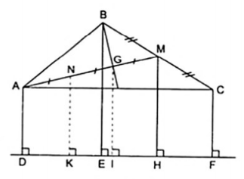
Tương tự câu a) ta có BE, MH, CF là ba đường thẳng song song cách đều nên chúng chắn trên đường thẳng d hai đoạn thẳng liên tiếp bằng nhau là EH = HF. Do đó MH là đường trung bình của hình thang BCFE.

Áp dụng định lí đường trung bình vào hình thang BCFE, thu được: BE + CF = 2MH.

Lại có AD, NK, GI, MH cũng là bốn đường thẳng song song cách đều nên chúng chắn trên đường thẳng d ba đoạn thẳng liên tiếp bằng nhau là: 

DK = KI = IH

Do đó NK, GI thứ tự là hai đường trung bình của hai hình thang AGID và NMHK. Áp dụng định lí đường trung bình vào hình thang này ta được:

AD + GI = 2NK và NK + MH = 2GI hay 2NH + 2MH = 4GI (2)

Thay 2MH = BE + CF và 2NK = AD + GI vào đẳng thức (2) ta được: 

AD + BE + CF = 3GI