Bài tập về vẽ thêm hình chữ nhật để tính độ dài đoạn thẳng, tính góc, chứng minh quan hệ về độ dài

3.

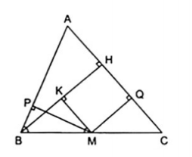
Kẻ MK $\perp $ BH thì ta được MK // AC và $\widehat{K}=\widehat{H}=\widehat{Q}=90^{\circ}$

Tứ giác MKHQ có ba góc vuông nên là hình chữ nhật.

$\Delta $BMP = $\Delta $MBK (cạnh huyền - góc nhọn) $\Rightarrow $ MP = BK (1)

Lại có MQ = HK (2) theo tính chất về cạnh của hình chữ nhật.

Từ (1) và (2) $\Rightarrow $ MP + MQ = BH

4. 

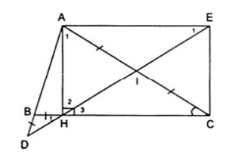
Đặt $\widehat{C}=a$ thì $\widehat{B}=2a$

a) Từ giả thiết BD = BH $\Rightarrow \widehat{D}=\widehat{BHD}$

Vì $\widehat{B}=2a$ là góc ngoài của $\Delta $BDH nên $\widehat{B}=2a=\widehat{D}+\widehat{BHD}$

$\Rightarrow \widehat{D}=\widehat{BHD}=a$.

Mà $\widehat{DHB}=\widehat{IHC}$ (hai góc đối đỉnh)

$\Rightarrow \widehat{ACH}=\widehat{IHC}=a$ (1)

$\Rightarrow \widehat{HAI}=\widehat{AHI}=90^{\circ}-a$ (2)

Từ (1) $\Rightarrow $ HI = IC

Từ (2) $\Rightarrow $ IA = IH

$\Rightarrow $ IH = IA = IC

Vậy IA = IC

b) Do I là trung điểm của AC nên chọn AC là một đường chéo

Vẽ thêm điểm E sao cho I là trung điểm của HE thì tứ giác AHCE là hình chữ nhật, vì có hai đường chéo cắt nhau tại trung điểm mỗi đường và có góc H vuông.

Áp dụng định nghĩa vào hình chữ nhật AHCE ta được HC // AE

$\Rightarrow \widehat{AEH}=\widehat{EHC}=a$ (so le trong)

Lại có $\widehat{D}=a$

$\Rightarrow \widehat{D}=\widehat{AEH}$

$\Rightarrow $ $\Delta $ADE cân tại A $\Rightarrow $ AE = AD.

Mà AE = HC $\Rightarrow $ AD = HC