Video giảng Toán 11 Cánh diều Chương VII bài 1 Định nghĩa đạo hàm. Ý nghĩa hình học của đạo hàm

Tóm lược nội dung

BÀI 1. ĐỊNH NGHĨA ĐẠO HÀM. Ý NGHĨA HÌNH HỌC CỦA ĐẠO HÀM (3 TIẾT)

Mến chào các em học sinh thân yêu!

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Nhận biết được một số bài toán dẫn đến khái niệm đạo hàm như: xác định vận tốc tức thời của một vật chuyển động không đều, xác định tốc độ thay đổi của nhiệt độ.
• Nhận biết được định nghĩa đạo hàm. Tính được đạo hàm của một số hàm đơn giản bằng định nghĩa.
• Nhận biết được ý nghĩa hình học của đạo hàm.
• Thiết lập được phương trình tiếp tuyến của đồ thị hàm số tại một điểm thuộc đồ thị.

HOẠT ĐỘNG KHỞI ĐỘNG

Trước khi vào bài học, chúng ta cùng trả lời câu hỏi sau: Xét hai hàm số:   Hàm số có đạo hàm tại x=0 là?

HOẠT ĐỘNG HÌNH THÀNH KIẾN THỨC

I. ĐẠO HÀM TẠI MỘT ĐIỂM

Nội dung 1. Một số bài toán dẫn đến khái niệm đạo hàm

Theo em, phương trình chuyển động của viên bi là gì?

 Video trình bày nội dung:

a) Bài toán tìm vận tốc tức thời

Phương trình chuyển động của viên bi là  

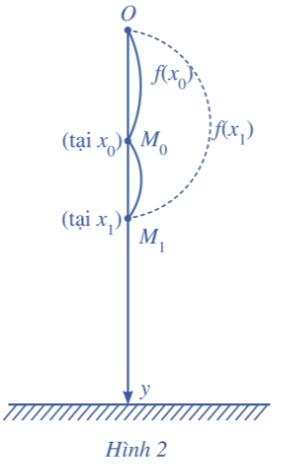
+ Tại thời điểm vật ở vị trí

; tại thời điểm vật ở vị trí

+ Quãng đường vật đi được: . Vận tốc trung bình của vật là

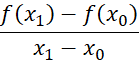
+ Nếu càng nhỏ thì tỉ số trên càng phản ánh rõ sự nhanh hay chậm của viên bi tại thời điểm đó.

b) Bài toán tìm cường độ tức thời

Điện lượng truyền trong dây dẫn là một hàm số của thời gian

+ Cường độ trung bình của dòng điện:

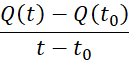
+ Nếu càng nhỏ thì tỉ số trên càng biểu thị chính xác cường độ dòng diện tại thời điểm .

Nội dung 2. Định nghĩa đạo hàm tại một điểm

Em hãy trình bày định nghĩa đạo hàm tại một điểm?

 Video trình bày nội dung:

HĐ1

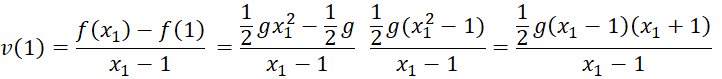
Định nghĩa: 

Cho hàm số xác định trên khoảng và điểm

Nếu tồn tại giới hạn thì giới hạn đó được gọi là đạo hàm của hàm số ) tại và được kí hiệu hoặc .

Nhận xét: Trong định nghĩa trên, ta đặt:

và gọi là số gia của biến số tại điểm . 

và gọi là số gia của hàm số ứng với số gia tại điểm .   

Khi đó, ta có: .

………..

Nội dung video bài 1: Định nghĩa đạo hàm, Ý nghĩa hình học của đạo hàm còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.