Video giảng Toán 11 Cánh diều Chương III bài 2 Giới hạn của hàm số

Tóm lược nội dung

BÀI 2: GIỚI HẠN CỦA HÀM SỐ

Xin chào các em học sinh thân mến, chúng ta lại gặp nhau trong bài học ngày hôm nay rồi!

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

• Nhận biết khái niệm giới hạn hữu hạn của hàm số, giới hạn hữu hạn một phía của hàm số tại một điểm.
• Nhận biết khái niệm giới hạn hữu hạn của hàm số tại vô cực và mô tả được một số giới hạn cơ bản như: với c là hằng số và k là số nguyên dương.
• Nhận biết khái niệm giới hạn vô cực của hàm số tại một điểm và hiểu được một số giới hạn cơ bản như:
• Tính một số dạng giới hạn của hàm số bằng cách vận dụng các phép toán trên giới hạn hàm số.
• Giải quyết một số vấn đề thực tiến gắn với giới hạn của hàm số.

HOẠT ĐỘNG KHỞI ĐỘNG

Trước khi bước vào bài học ngày hôm nay, các em trả lời cho cô câu hỏi: Giá trị của giới hạn  là?

HOẠT ĐỘNG KHÁM PHÁ

Nội dung 1: Giới hạn hữu hạn của hàm số tại một điểm

Theo em: Ta nói hàm số  có giới hạn là ?

Video trình bày nội dung:

a) Khi  càng gần đến 1 thì giá trị của hàm số càng gần đến 4 .

b) Điểm  càng gần đến điểm  trên trục tung khi điểm  càng gần về điểm  trên trục hoành.

*) Sử dụng giới hạn dãy số

Lấy dãy số  bất kì sao cho ta có

Do đó,

Ta nói hàm số  có giới hạn là 4 khi x dần tới 1.

Kết luận:

Cho điểm  thuộc khoảng K và hàm số  xác định trên K hoặc . Ta nói hàm số  có giới hạn là số  khi  dần tới  nếu với dãy số  bất kì,  và , thì , kí hiệu  hay
khi . 

Nội dung 2: Các phép toán về giới hạn hữu hạn của hàm số

Em hãy nêu các phép toán về giới hạn hữu hạn của hàm số?

Video trình bày nội dung:

HĐKP 2

a) Ta có

.

b) Vì  

nên .

Ta có:

.

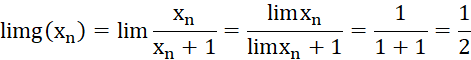
Do đó .

Từ (1) và (2) suy ra 

.

Kết luận

+ Cho  và. Khi đó

+ Nếu  và

thì  và .

(Dấu của f(x) được xét trên khoảng tìm giới hạn,

Nhận xét:a) k là số nguyên dương;

b)  nếu tồn tại

………..

Nội dung video Bài 2: Giới hạn của hàm số còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.