Slide bài giảng toán 10 chân trời sáng tạo bài 3: Tích của một số với một vectơ
Slide điện tử bài 3: Tích của một số với một vectơ. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 10 Chân trời sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3. TÍCH CỦA MỘT SỐ VỚI MỘT VECTO
1. TÍCH CỦA MỘT SỐ VỚI MỘT VECTƠ VÀ CÁC TÍNH CHẤT
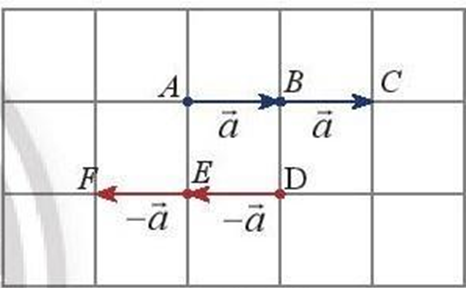
Bài 1: Cho vectơ 
. Hãy xác định độ dài và hướng của hai vectơ: 
, (−
) + (−
).
Trả lời rút gọn:
=
, vectơ 
+ 
cùng hướng với vectơ 
= 
, vectơ (
) + 
ngược hướng với 
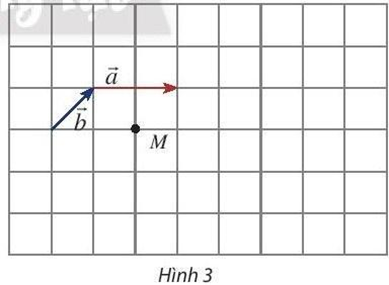
Bài 2: Cho hai vectơ 
, 
và một điểm M như Hình 3.
a. Hãy vẽ các vectơ 
b. Cho biết mỗi ô vuông có cạnh bằng 1. Tính: 
, 
, 
Trả lời rút gọn:
a.
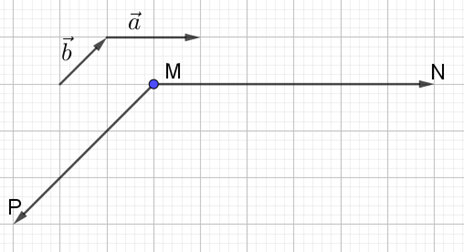
b) 
= 
= 
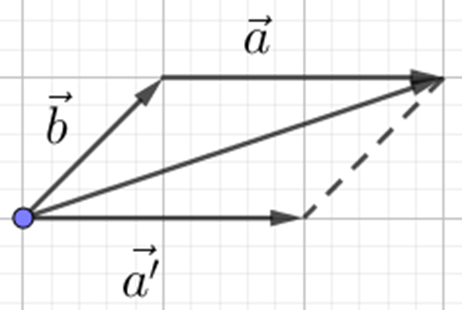
Có: 
= 
= 
= 2
Bài 3: Cho tam giác ABC. Chứng minh G là trọng tâm của tam giác ABC khi và chỉ khi 
+ 
+ 
= 3
Trả lời rút gọn:
G là trọng tâm tam giác ABC
+ 
+ 
= 
- 
+ 
- 
+ 
- 
= 
+ 
+ 
- 3
= 
+ 
+ 
= 3
(đpcm)
Bài 4: Một con tàu chở hàng A đang đi về hướng Tây với tốc độ 20 hải lí/giờ. Cùng lúc đó, một con tàu chở khách B đang đi về hướng đông với tốc độ 50 hải lí/giờ. Biếu diễn vectơ 
của tàu B theo vectơ vận tốc 
của tàu A.
Trả lời rút gọn:
= 
2. ĐIỀU KIỆN ĐỂ HAI VECTƠ CÙNG HƯỚNG
Bài 1: Cho hai vectơ 
và 
cùng phương, 
khác 
và cho 
= 
. So sánh độ dài và hướng của hai vectơ 
và 
Trả lời rút gọn:
, 
cùng hướng với nhau
Bài 2: Cho tứ giác ABCD có I và J lần lượt là trung điểm của AB và CD. Cho điểm G thỏa mãn 
+ 
+ 
+ 
= 
. Chứng minh ba điểm I, G, J thẳng hàng.
Trả lời rút gọn:
Ta có: 
+ 
+ 
+ 
= 
- 
+ 
- 
+ 
- 
+ 
- 
= 
(
+ 
) - 2
+ (
+ 
) - 2
= 
- 2
+ 
- 2
= 
( I, J là trung điểm của AB, DC)
= - 
Ba điểm I, J, G thẳng hàng.
BÀI TẬP CUỐI SGK
Bài 1. Cho hình bình hành ABCD có O là giao điểm hai đường chéo. Với M là điểm tùy ý, chứng minh rằng:
a. 
+ 
+ 
+ 
= 4
b. 
+ 
+ 
= 2
Trả lời rút gọn:
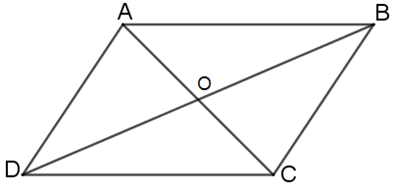
a. Ta có: O là giao điểm hai đường chéo của hình bình hành ABCD 
+ 
+ 
+ 
= 
- 
+ 
- 
+ 
- 
+ 
- 
= 
+ 
+ 
+ 
= 4
b. 
+ 
= 
(quy tắc hình bình hành)
+ 
+ 
= 2
Bài 2. Cho tứ giác ABCD. Gọi M và N lần lượt là trung điểm của các cạnh AB và CD. Chứng minh rằng:
a. 
b. 
Trả lời rút gọn:
a. 
(M là trung điểm của AB); 
(N là trung điểm của CD).
VT = 
= 
b. Giả sử: 
⬄ 
⬄ 
⬄ 
(luôn đúng)
Vậy 
Bài 3. Cho hai điểm phân biệt A và B. Xác định điểm M sao cho 
Trả lời rút gọn:
M nằm giữa A và B ; 
.
Bài 4. Cho tứ giác ABCD. Gọi E, F, G lần lượt là trung điểm của các đoạn thẳng AB, CD, EF. Lấy điểm M tùy ý, chứng minh rằng 
Trả lời rút gọn:
Xét VT = 
= 
+ 
+ 
+ 
+ 
+ 
+ 
+ 
= 2
+ (
+ 
) + 2
+ (
+ 
)
= 2
+ 
+ 2
+ 
(E, F là trung điểm của AB, CD)
= 2(
+ 
) = 2(
+ 
+ 
+ 
)
= 4
+ 2.
(G là trung điểm của EF)
= 4
= VP
Vậy 
+ 
+ 
+ 
= 4
Bài 5. Máy bay A đang bay về hướng đông bắc với tốc độ 600 km/h. Cùng lúc đó, máy bay B đang bay về hướng tây nam với tốc độ 800km/h. Biểu diễn vectơ vận tốc 
của máy bay B theo vectơ vận tốc 
của máy bay A.
Trả lời rút gọn:
Tốc độ của máy bay B so với A là: 800 : 600 = 
=
Có: 
cùng phương ngược chiều với 
Bài 6. Cho hai điểm phân biệt A và B.
a. Xác định điểm O sao cho 
b. Chứng minh rằng với mọi điểm M, ta có 
Trả lời rút gọn:
a. O trên đoạn thẳng AB sao cho OA = 3OB
b. 
⬄ 
⬄
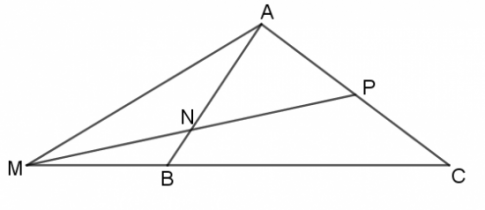
Bài 7. Cho tam giác ABC.
a. Xác định điểm M, N thảo mãn 
b. Biểu thị mỗi vectơ 
theo hai vectơ 
c. Chứng minh ba điểm M, N, P thẳng hàng.
Trả lời rút gọn:
a)
M nằm ngoài đoạn thẳng BC sao cho BC = 2BM N nằm trên đoạn thẳng AB sao cho AN = 3BN P là trung điểm đoạn thẳng AC. |
b)
|
c) Theo phần b, ta thấy: |
Slide bài giảng lớp 10 cánh diều
Slide bài giảng lớp 10 chân trời sáng tạo
Slide bài giảng lớp 10 kết nối tri thức
