Slide bài giảng toán 10 chân trời bài 3: Giải tam giác và ứng dụng thực tế

Tóm lược nội dung

BÀI 3: GIẢI TAM GIÁC VÀ ỨNG DỤNG THỰC TẾ

KHỞI ĐỘNG

Với số liệu đo được từ một bên bờ sông như hình vẽ sau, bạn hãy giúp nhân viên đo đạc tính khoảng cách giữa hai cái cây bên kia bờ sông.

Trả lời rút gọn: 

Định lí côsin, có:

Khoảng cách giữa hai cây là: 

53,9 (m)

1. GIẢI TAM GIÁC

Bài 1: Giải tam giác ABC trong các trường hợp sau:

a. a = 17,4;

b. a = 10; b = 6; c = 8

Trả lời rút gọn: 

2. ÁP DỤNG GIẢI BÀI TOÁN VÀO THỰC TẾ

Bài 1: Hai máy bay cùng cất cánh từ một sân bay nhưng bay theo hai hướng khác nhau. Một chiếc di chuyển với tốc độ 450 km/h theo hướng tây và chiếc còn lại di chuyển theo hướng lệch so với hướng bắc 25 về phía tây với tốc độ 630km/h (Hình 5). Sau 90 phút, hai máy bay cách nhau bao nhiêu kilomet? Giả sử chúng đang ở cùng độ cao.

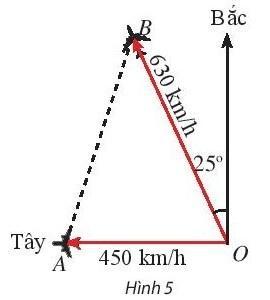
Trả lời rút gọn: 

Đổi 90' = 1,5h

Quãng đường máy bay 1 bay được sau 90p là: OA = 450.1,5 = 675 (km)

Quãng đường máy bay 2 bay được sau 90p là: OB = 630. 1,5 = 945 (km)

Có: = 90 - 25 = 65

Định lí côsin, ta có:

AB² = OA² + OB² - 2. OA. OB. cos

= 675² + 945² - 2. 675. 945. cos65

≈ 809494,75 AB ≈ 889,7 (km)

Vậy sau 90 phút, hai máy bay cách nhau khoảng 899,7 km.

Bài 2: Trên bản đồ địa lí, người ta thường gọi tứ giác với bốn đỉnh lần lượt là các thành phố Hà Tiên, Châu Đốc, Long Xuyên, Rạch Giá là tứ giác Long Xuyên. Dựa theo các khoảng cách đã cho trên Hình 6, tính khoảng cách giữa Châu Đốc và Rạch Giá.

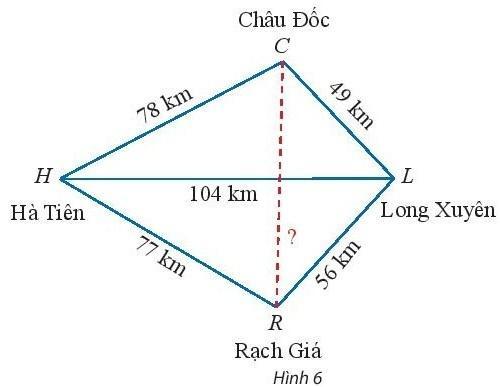
Trả lời rút gọn: 

Hệ quả định lí côsin, ta có:

= + ≈ 2639’ + 3149’ = 5828’

Định lí côsin, ta có:

CR² = HC² + HR²  - 2HC. HR. cos

= 78² + 77² - 78. 77. cos5828’ ≈ 5730,79

CR ≈ 75,7 (km)

Vậy Châu Đốc và Rạch Giá cách nhau khoảng 75,7 km.

BÀI TẬP CUỐI SGK

Bài 1. Giải tam giác ABC trong các trường hợp sau:

a. AB = 14; AC = 23, .

b. BC = 22, 

c. AC = 22,  = 120; = 28

d. AB = 23; AC = 32; BC = 44.

Trả lời rút gọn: 

a) .

Định lí côsin, ta có:

BC² = AB² + AC² - 2. AB. AC. cosA = 14² + 23² - 2. 14. 23.cos125 ≈ 1 094,38

BC ≈ 33,08.

Định lí sin, ta có:

Vì =>

b)

Định lí sin, ta có:

=> AB ≈ 13,85; AC ≈ 20,22.

c) AC = 22; = 120; = 28

= 180 - - = 180 - 120 - 28 = 32

Định lí sin, ta có:

=> BC ≈ 13,46; AB ≈ 11,93.

d) AB = 23; AC = 32; BC = 44.

Hệ quả định lí côsin, ta có:

Định lí sin, ta có:

Vì => . 

Bài 2. Để lắp đường dây điện cao thế từ vị trí A đến vị trí B, do phải tránh một ngọn núi nên người ta phải nối đường dây từ vị trí A đến vị trí C dài 10 km, sau đó nối đường dây từ vị trí C đến vị trí B dài 8km. Góc tạo bởi hai đoạn dây AC và CB là 70∘. Tính chiều dài tăng thêm vì không thể nối trực tiếp từ A đến B. 

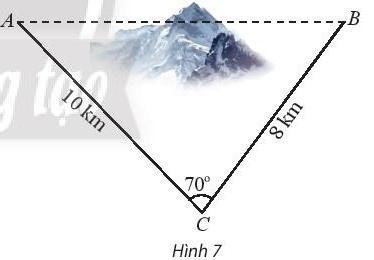
Trả lời rút gọn: 

Định lí côsin, ta có:

Vậy tốn thêm (km).

Bài 3. Một người đứng cách thân một cái quạt gió 16m và nhìn thầy tâm của cánh quạt với góc nâng 56,5 (Hình 8). Tính khoảng cách từ tâm của cánh quạt đến mặt đất. Cho biết khoảng cách từ mắt của người đó đến mặt đât là 1,5m.

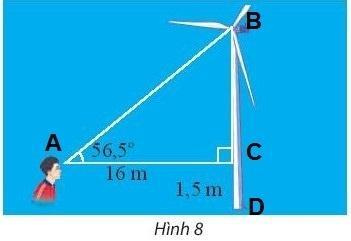
Trả lời rút gọn: 

Khoảng cách từ tâm của cánh quạt đến mặt đất:

Bài 4. Tính chiều cao AB của một ngọn núi. Biết tại hai điểm C, D cách nhau 1 km trên mặt đất (B, C, D thẳng hàng), người ta nhìn thấy đỉnh A của núi với góc nâng lần lượt là 32 và 40 (Hình 9).

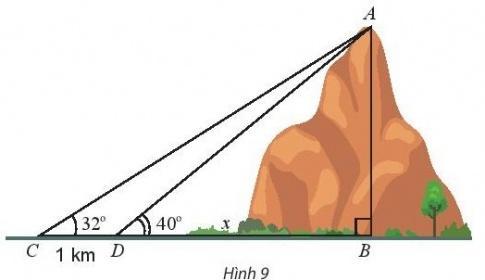
Trả lời rút gọn: 

Ta có: .

Định lí sin trong , ta có:

, ta có:

Bài 5. Hai người quan sát khinh khí cầu tại hai điểm P và Q nằm ở sườn đồi nghiêng 32 so với phương ngang, cách nhau 60m (Hình 10). Người quan sát tại P xác định góc nâng của khinh khí cầu là 62. Cùng lúc đó, người quan sát tại Q xác định góc nâng của khinh khí cầu là 70. Tính khoảng cách từ Q đến khinh khí cầu.

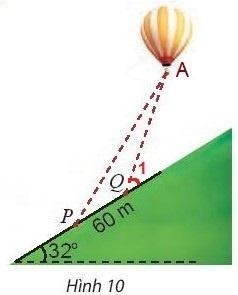
Trả lời rút gọn: 

,

Định lí sin cho , có:

Bài 6. Một người đứng ở trên một tháp truyền hình cao 352 m so với mặt đất, muốn xác định khoảng cách giữa hai cột mốc trên mặt đất bên dưới. Người đó quan sát thấy góc được tạo bởi hai đường ngắm tới hai mốc này là 43, góc giữa phương thẳng đứng và đường ngắm tới một điểm mốc trên mặt đất là 62 và điểm mốc khác là 54 (Hình 11). Tính khoảng cách giữa hai cột mốc này.

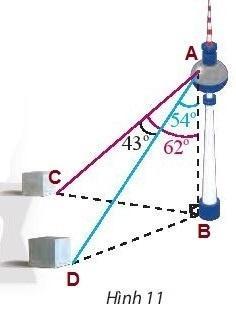
Trả lời rút gọn: 

,

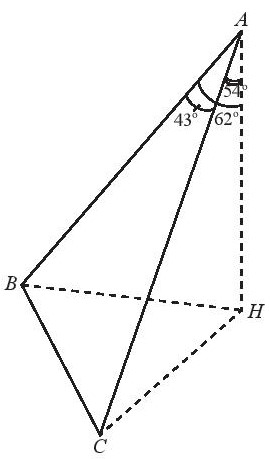
Định lí côsin trong , có: