Slide bài giảng toán 10 chân trời bài 3: Các số đặc trưng đo xu thế trung tâm của mẫu số liệu

Tóm lược nội dung

BÀI 3. CÁC SỐ ĐẶC TRƯNG ĐO XU THẾ TRUNG TÂM CỦA MẪU SỐ LIỆU

1. SỐ TRUNG BÌNH

Bài 1: Điểm số bài kiểm tra môn Toán của các bạn trong Tổ 1 là 6; 10; 6; 8; 7; 10, còn của các bạn Tổ 2 là 10; 6; 9; 9; 8; 9. Theo em, tổ nào có kết quả kiểm tra tốt hơn tại sao?

Trả lời rút gọn: 

=> Kết quả kiểm tra của Tổ 2 tốt hơn.

Bài 2: Thời gian chạy 100 mét (đơn vị: giây) của các bạn học sinh ở hai nhóm A và B được ghi lại ở bảng:

Nhóm nào có thành tích chạy tốt hơn?

Trả lời rút gọn:

Bài 3: Số bàn thắng mà một đội bóng ghi được ở mỗi trận đấu trong một mùa giải được thống kê lại ở bảng sau:

Hãy xác định số bàn thắng trung bình đội đó ghi được trong một trận đấu của mùa giải.

Trả lời rút gọn: 

Số bàn thắng trung bình đội ghi được trong một trận đấu của mùa giải :

   ≈ 0,62 (bàn thắng)

2. TRUNG VỊ VÀ TỨ PHÂN VỊ

Bài 1: Bảng sau thống kê số sách mỗi bạn học sinh Tổ 1 và Tổ 2 đã đọc ở thư viện trường trong một tháng:

a. Trung bình mỗi bạn Tổ 1 và mỗi bạn Tổ 2 đọc bao nhiêu quyển sách ở thư viện trường trong tháng đó.

b. Em hãy thảo luận với các bạn trong nhóm xem tổ nào chăm đọc sách ở thư viện hơn.

Trả lời rút gọn: 

a. 

Trung bình mỗi bạn Tổ 1 đọc được: ≈ 4,44(quyển sách)

Trung bình mỗi bạn Tổ 2 đọc được: = 4

b. Tổ 2 đọc nhiều sách hơn Tổ 1.

Bài 2: Hãy tìm trung vị của các số liệu ở Vận dụng 1 và Vận dụng 2.

Trả lời rút gọn: 

Sắp xếp số giây các bạn nhóm A chạy được theo thứ tự không giảm, ta được dãy: 

12,2; 12,5; 12,7; 12,8; 12,9; 13,1; 13,2; 13,5

Cỡ mẫu = 8 nên trung vị của A là trung bình cộng của số liệu thứ 4 , 5 của dãy trên. Vậy Me = (12,8 + 12,9) = 12,85

Sắp xếp số giây nhóm A chạy được theo thứ tự không giảm: 12,1; 12,9; 13,2; 13,4; 13,7.

Cỡ mẫu = 5 nên trung vị của B là số liệu thứ 3 của dãy trên. Vậy Me = 13,2.

Cỡ mẫu = 26. Sắp xếp số bàn thắng theo thứ tự không giảm thì số liệu thứ 13;14 là 1; 1. Vậy Me = (1+1) = 1.

Bài 3: Cân nặng của 20 vận động viên môn vật của một câu lạc bộ được ghi lại ở bảng sau:

Để thuận tiện cho việc luyện tập, ban huấn luyện muốn xếp 20 vận động viên trên thành 4 nhóm, mỗi nhóm gồm 25% số vận động viên có cân nặng gần nhau. Bạn hãy giúp ban huấn luyện xác định các ngưỡng cân nặng để phân nhóm mỗi vận động viên.

Trả lời rút gọn: 

Sắp xếp số cân nặng theo theo thứ tự không giảm:

50; 52; 52; 54; 54; 56; 56; 57; 58; 58; 59; 61; 61; 62; 64; 65; 66; 67; 68; 69

Cỡ mẫu: n = 20 (chẵn) nên giá trị tứ phân vị thứ hai là: 

Q2 = (58 + 59) = 58,5.

Tứ phân vị thứ nhất là trung vị của mẫu: 50; 52; 52; 54; 54; 56; 56; 57; 58. 

 Q1 = (54 + 56) = 55.

Tứ phân vị thứ ba là trung vị của mẫu: 59; 61; 61; 62; 64; 65; 66; 67; 68; 69. 

Q3 = (64 + 65) = 64,5

Vậy huấn luyện viên phân nhóm vận động viên là: 55; 58,5 và 64,5.

Bài 4: Hãy tìm tứ phân vị của các mẫu số liệu sau:

a. 10; 13; 15; 2; 10; 19; 2; 5; 7.

b. 15; 19; 10; 5; 9; 10; 1; 2; 5; 15

Trả lời rút gọn: 

a. Sắp xếp lại mẫu số liệu theo thứ tự không giảm: 2; 2; 5; 7; 10; 10; 13; 15; 19.

Cỡ mẫu: n = 9, là số lẻ, nên giá trị tứ vị phân thứ hai:

Q₂ = 10.

Tứ phân vị thứ nhất là trung vị của mẫu: 2; 2; 5; 7. 

Q₁ = (2 + 5) = 3,5.

Tứ phân vị thứ ba là trung vị của mẫu: 10; 13; 15; 19. 

Q₃ = (13 + 15) = 14

b. Sắp xếp lại mẫu số liệu theo thứ tự không giảm, ta được: 1; 2; 5; 5; 9; 10; 10; 15; 15; 19.

Cỡ mẫu: n = 10 (chẵn), nên giá trị tứ vị phân thứ hai: 

Q₂ = (9 + 10) = 9,5.

Tứ phân vị thứ nhất là trung vị của mẫu: 1; 2; 5; 5; 9.

Q₁ = 5.

Tứ phân vị thứ ba là trung vị của mẫu: 10; 10; 15; 15; 19. 

Q₃ = 15.

3. MỐT

Bài 1: Một cửa hàng kinh doanh hoa thống kê số hoa hồng bán được trong ngày 14 tháng 2 theo loại hoa và thu được bảng tần số sau:

Cửa hàng nên nhập loại hoa nào nhiều nhất để bán trong ngày 14 tháng 2 năm tiếp theo? Tại sao?

Trả lời rút gọn: 

Số lượng hoa hồng nhung bán được nhiều nhất (230 bông). 

=> Cửa hàng nên nhập hoa hồng nhung để bán trong ngày 14 tháng 2 năm tiếp theo.

Bài 2: Hãy tìm mốt của số liệu điểm kiểm tra của các bạn Tổ 1 trong Khám phá 1.

Trả lời rút gọn: 

Mẫu số liệu điểm kiểm tra của Tổ 1 : Mo = 6; 10.

BÀI TẬP CUỐI SGK

Bài 1. Hãy tìm số trung bình, tứ phân vị và mốt của các mẫu số liệu sau:

a. 23; 41; 71; 29; 48; 45; 72; 41.

b. 12; 32; 93; 78; 24; 12; 54; 66; 78.

Trả lời rút gọn: 

a. Số trung bình của mẫu là: = (23 + 41 + 71 + 29 + 48 + 45 + 72 + 41) = 46,25

Sắp xếp lại mẫu số liệu theo thứ tự không giảm: 23; 29; 41; 41; 45; 48; 71; 72.

Do 41 xuất hiện hai lần, nhiều hơn các số còn lại nên mẫu số liệu trên có = 41.

b. Số trung bình của mẫu là:

  = (12 + 32 + 93 + 78 + 24 + 12 + 54 + 66 + 78) 48,89.

Sắp xếp lại mẫu số liệu theo thứ tự không giảm: 12; 12; 24; 32; 54; 66; 78; 78; 93.

Vì 12 và 78 xuất hiện hai lần nên mẫu số liệu trên có = 12; 78.

Bài 2. Hãy tìm số trung bình, tứ vị phân và mốt của các số liệu sau:

Trả lời rút gọn: 

a. Số trung bình của mẫu: = (23 + 25 + 28 + 31 + 33 + 37) 4,78.

Cỡ mẫu là n = 37 (lẻ). Sắp xếp các số liệu theo thứ tự không giảm thì số liệu thứ 19 là 28. Giá trị tứ phân vị thứ hai là = 28.

Tứ phân vị thứ nhất là trung vị của mẫu:

Cỡ mẫu = 18 (chẵn) . Số liệu thứ 9 và 10 lần lượt là 25; 25.Giá trị tứ phân vị thứ nhất: = (25 + 25) = 25. 

Tứ phân vị thứ ba là trung vị của mẫu:

Cỡ mẫu là 18, là một số chẵn. Số liệu thứ 9 và 10 lần lượt là 31; 31. Giá trị tứ phân vị thứ ba: = (31 + 31) = 31.

Tần số của giá trị 28 là 10, lớn hơn tần số của các giá trị còn lại nên mẫu số liệu trên có = 28.

b. Số trung bình của mẫu là: = = 11

• Giá trị tứ phân vị thứ hai: = (0 + 0) = 0

• Giá trị tứ phân vị thứ nhất: 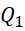= 0

• Giá trị tứ phân vị thứ ba: = 2

Tần số tương đối của giá trị 0 là 0,6; lớn hơn tần số tương đối của các giá trị còn lại nên mẫu số liệu trên có = 0

Bài 3. An lấy ra ngẫu nhiên 3 quả bóng từ một hộp có chứa nhiều bóng xanh và bóng đỏ. An đếm xem có bao nhiêu bóng đỏ trong 3 bóng lấy ra đó rồi trả bóng lại hộp. An lặp lại phép thử trên 100 lần và ghi lại kết quả ở bảng sau:

Hãy tìm số trung bình, tứ phân vị và mốt của bảng kết quả trên.

Trả lời rút gọn: 

Số trung bình của mẫu: = (0 + 1 + 2 + 3) = 0,06.

Cỡ mẫu n = 100, số liệu thứ 50 và 51 lần lượt là 2; 2. Giá trị tứ phân vị thứ hai: = (2 + 2) = 2.

Tứ phân vị thứ nhất là trung vị của mẫu:

Cỡ mẫu = 50, số liệu thứ 25 và 26 đều là 1. Giá trị tứ phân vị thứ nhất: = 1.

Tứ phân vị thứ ba là trung vị của mẫu:

Cỡ mẫu = 50, số liệu thứ 25 và 26 đều là 2. Giá trị tứ vị phân thứ ba: = 2.

Có 40 lần An lấy được 2 quả bóng đỏ, nhiều hơn số lần lấy được 0, 1, 3 quả bóng đỏ nên mẫu trên có = 2

Bài 4. Trong một cuộc thi nghề, người ta ghi lại thời gian hoàn thành một sản phẩm của một số thí sinh ở bảng sau:

a. Hãy tìm số trung bình, tứ phân vị và mốt của thời gian thi nghề của các thí sinh trên.

b. Năm ngoái, thời gian thi của các thí sinh có số trung bình và số trung vị đều bằng 7. Bạn hãy so sánh thời gian thi nói chung của các thí sinh trong hai năm.

Trả lời rút gọn: 

a. Thời gian thi nghề trung bình: (5 + 6 + 7 + 8 + 35) 5,08.

Cỡ mẫu n = 12 (chẵn). Giá trị tứ phân vị thứ hai : = (7 + 7) = 7.

Tứ phân vị thứ nhất là trung vị của mẫu: 5; 6; 6; 6; 7; 7. 

= (6 + 6) = 6.

Tứ phân vị thứ ba là trung vị của mẫu: 7; 7; 7; 8; 8; 35. 

= (7 + 8) = 7,5.

Số thí sinh thi 7 phút là 5 học sinh > số thí sinh có thời gian hoàn thành bài thi trong 5, 6, 8 và 35 phút nên mẫu trên có = 7.

b. Vì thời gian thi trung bình của năm nay (5,08 phút) < thời gian thi trung bình của năm ngoái (7 phút) => thời gian thi của các thí sinh năm nay ít hơn so với năm trước.

Bài 5. Bác Dũng và bác Thu ghi lại số cuộc điện thoại mà mỗi người gọi mỗi ngày trong 10 ngày được lựa chọn ngẫu nhiên từ tháng 01/2021 ở bảng sau:

a. Hãy tìm số trung bình, tứ phân vị và mốt của số cuộc điện thoại mà mỗi bác gọi theo số liệu trên.

b. Nếu so sánh theo số trung bình thì ai có nhiều cuộc điện thoại hơn?

c. Nếu so sánh theo số trung vị thì ai có nhiều cuộc điện thoại hơn?

d. Theo bạn, nên dùng số trung bình hay số trung vị để so sánh xem ai có nhiều cuộc điện thoại hơn mỗi ngày?

Trả lời rút gọn: 

a. Trung bình số cuộc điện thoại mà bác Dũng gọi trong 10 ngày là:

= (2 + 7 + 3 + 6 + 1 + 4 + 1 + 4 + 5 + 1) = 3,4 (cuộc)

Sắp xếp lại số cuộc điện thoại mà bác Dũng gọi mỗi ngày theo thứ tự không giảm: 1; 1; 1; 2; 3; 4; 4; 5; 6; 7.

• Vì cỡ mẫu n = 10 (chẵn), giá trị tứ phân vị thứ hai: 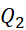= (3 + 4) = 7,5

• Tứ phân vị thứ nhất là trung vị của mẫu: 1; 1; 1; 2; 3. = 1

• Tứ phân vị thứ ba là trung vị của mẫu: 4; 4; 5; 6; 7. 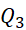= 5

Số ngày bác Dũng gọi 1 cuộc điện thoại là 3 > số ngày bác thực hiện số cuộc điện thoại khác, nên mẫu trên có = 1.

Trung bình số cuộc điện thoại bác Thu gọi trong 10 ngày là: 

= (1 + 3 + 1 + 2 + 3 + 4 + 1 + 2 + 20 + 2) = 3,9 (cuộc)

Sắp xếp lại số cuộc điện thoại mà bác Thu gọi mỗi ngày theo thứ tự không giảm: 1; 1; 1; 2; 2; 2; 3; 3; 4; 20.

• Vì cỡ mẫu n = 10 (chẵn), giá trị tứ phân vị thứ hai 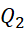= (2 + 2) = 2

• Tứ phân vị thứ nhất là trung vị của mẫu: 1; 1; 1; 2; 2. 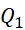= 1

• Tứ phân vị thứ ba là trung vị của mẫu: 2; 3; 3; 4; 20. = 3

Số ngày bác Thu gọi 1 cuộc điện thoại và 2 cuộc điện thoại là 3 > số ngày bác thực hiện số cuộc điện thoại khác, nên mẫu trên có = 1; 2.

b. Nếu so sánh số trung bình, bác Thu gọi nhiều cuộc điện thoại hơn.

c. Nếu so sánh số trung vị, bác Dũng có nhiều cuộc điện thoại hơn.

d. Nên dùng số trung vị để so sánh vì bác Thu có một số liệu quá lớn so với các số liệu còn lại.

Bài 6. Tổng số điểm mà các thành viên đội tuyển Olympic Toán quốc tế (IMO) của Việt Nam đạt được trong 20 kì thi được cho ở bảng sau:

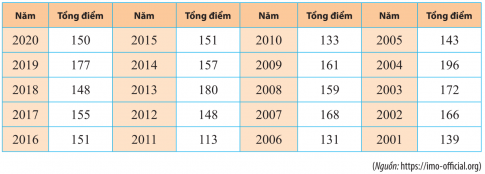
Có ý kiến cho rằng điểm thi của đội tuyển giai đoạn 2001 - 2010 cao hơn giai đoạn 2011- 2020. Hãy sử dụng số trung bình và trung vị để kiểm nghiệm xem ý kiến trên có đúng không?

Trả lời rút gọn: 

Bài 7. Kết quả bài kiểm tra giữa kì của các bạn học sinh lớp 10A, 10B, 10C được thống kê ở các biểu đồ dưới đây.

a. Hãy lập bảng thống kê số lượng học sinh theo điểm số ở mỗi lớp.

b. Hãy so sánh điểm số của học sinh các lớp đó theo số trung bình, trung vị và mốt.

Trả lời rút gọn: 

a. Bảng thống kê số lượng học sinh theo điểm số ở mỗi lớp

b. Điểm số trung bình lớp 10A: = 8,35

Điểm số trung bình lớp 10B: = 7,5

Điểm số trung bình lớp 10C: = 7,6

Điểm số của học sinh lớp 10A là cao nhất, lớp 10B là thấp nhất.

Lớp 10A: Cỡ mẫu n = 40. Sắp xếp điểm số theo thứ tự không giảm thì số liệu thứ 20, 21 của dãy đều là 9. Trung vị của dãy = 9

Lớp 10B: Cỡ mẫu n = 40. Sắp xếp điểm số theo thứ tự không giảm thì số liệu thứ 20, 21 của dãy lần lượt là 7, 8. Trung vị của dãy = (7 + 8) = 7,5

Lớp 10C: Cỡ mẫu n = 40. Sắp xếp điểm số theo thứ tự không giảm thì số liệu thứ 20, 21 của dãy đều là 7 . Trung vị của dãy = 7

Điểm số của các học sinh lớp 10A là cao nhất, lớp 10C là thấp nhất.

Lớp 10A: số học sinh có điểm 9 là 14, cao nhất so với các điểm còn lại nên = 9

Lớp 10B: số học sinh có điểm 7, 8 là 10, cao nhất so với các điểm còn lại nên = 7, 8

Lớp 10C: số học sinh có điểm 7 là 17, cao nhất so với các điểm còn lại nên = 7

Điểm số của các học sinh lớp 10A là cao nhất, lớp 10C là thấp nhất.