Slide bài giảng toán 10 chân trời sáng tạo bài 1: Hàm số và đồ thị
Slide điện tử bài 1: Hàm số và đồ thị. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 10 Chân trời sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1. HÀM SỐ VÀ ĐỒ THỊ
KHỞI ĐỘNG
Nhiệt độ có mối liên hệ gì với thời gian?

Trả lời rút gọn:
Thời gian thay đổi thì nhiệt độ thay đổi.
1. HÀM SỐ. TẬP XÁC ĐỊNH VÀ TẬP GIÁ TRỊ CỦA HÀM SỐ
Bài 1: Bản tin dự báo thời tiết cho biết nhiệt độ ở một số thời điểm trong ngày 1/5/2021 tại Thành phố Hồ Chí Minh đã được ghi lại thành bảng kèm với biểu đồ bên:
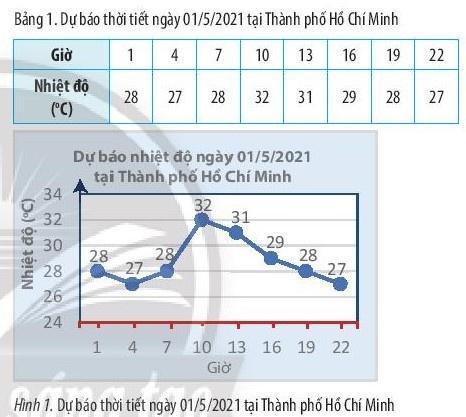
Sử dụng bảng hoặc biểu đồ, hãy:
a. Viết tập hợp các mốc giờ đã có dự báo nhiệt độ.
b. Viết tập hợp các số đo nhiệt độ đã dự báo.
c. Cho biết nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 1/5/2021.
Trả lời rút gọn:
a) Tập hợp các mốc giờ đã có dự báo nhiệt độ là: A = {1; 4; 7; 10; 13; 16; 19; 22} |
b) Tập hợp các số đo nhiệt độ đã dự báo là: B = {28; 27; 32; 31; 29; 28; 27} |
c) Nhiệt độ dự báo tại Thành phố Hồ Chí Minh vào lúc 7 giờ sáng ngày 01/5/2021 là: 28oC. |
Bài 2: Một thiết bị đã ghi lại vận tốc v (mét/giây) ở thời điểm t (giây) của một vật chuyển động như trong bảng sau:
t (giây) | 0,5 | 1 | 1,2 | 1,8 | 2,5 |
v (mét/giây) | 1,5 | 3 | 0 | 5,4 | 7,5 |
Vì sao bảng này biểu thị một số hàm số? Tìm tập xác định của hàm số này.
Trả lời rút gọn:
Ứng với mỗi thời điểm t(giây) trong bảng đều có một giá trị vận tốc v(mét/giây). Vì vậy, bảng này biểu thị một hàm số.
Hàm số đó có tập xác định D = {0,5; 1; 1,2; 1,8; 2,5}.
Bài 3: Tìm tập xác định của các hàm số sau:
a. ![]() b.
b. ![]()
Trả lời rút gọn:
a) ![]()
Biểu thức ![]() có nghĩa
có nghĩa ![]()
Vậy TXĐ của hàm số: ![]()
b) ![]()
Biểu thức ![]() có nghĩa
có nghĩa ![]()
![]()
Vậy TXĐ của hàm số: ![]()
Bài 4: Ở góc của miếng đất hình chữ nhật, người ta làm một bồn hoa có dạng một phần tư hình tròn với bán kính r (Hình 2). Bán kính bồn hoa có kích thước từ 0,5m đến 3m.

a. Viết công thức của hàm số biểu thị diện tích bồn hoa theo bán kính r và tìm tập xác định của hàm số này.
b. Bán kính của bồn hoa bằng bao nhiêu thì nó có diện tích là 0,5![]() ?
?
Trả lời rút gọn:
a) Công thức biểu thị diện tích bồn hoa theo bán kính r là :
![]()
Tập xác định của hàm số : ![]()
b) ![]()
![]()
![]()
![]() (cm) ( r ∈ [0,5 ; 3] )
(cm) ( r ∈ [0,5 ; 3] )
2. ĐỒ THỊ HÀM SỐ
Bài 1: Xét hàm số y = f(x) cho bởi bảng sau:
x | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
f(x) | 8 | 3 | 0 | -1 | 0 | 3 | 8 |
a. Tìm tập xác định D của hàm số trên.
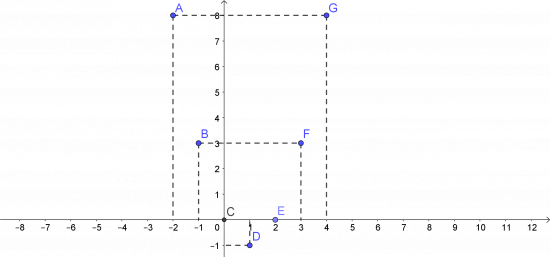
b. Trong mặt phẳng tọa độ Oxy, vẽ tất cả các điểm có tọa độ (x; y) với x ∈ D và y = f(x).
Trả lời rút gọn:
a. TXĐ của D = {-2; -1; 0; 1; 2; 3; 4}
b.
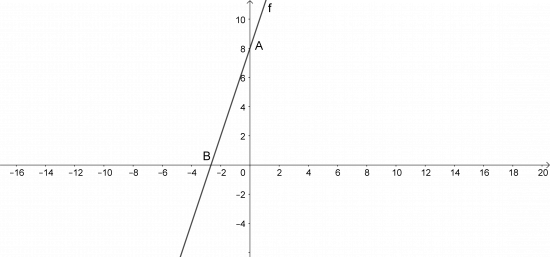
Bài 2: Vẽ đồ thị hàm số f(x) = 3x + 8
Trả lời rút gọn:
x = 0 => f(0) = 8. Có A(0; 8)
x = −
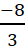 => f(
=> f(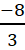 ) = 0. Có B(
) = 0. Có B(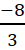 ; 0)
; 0)
Vẽ f qua A và B, có f là đồ thị của hàm số f(x) = 3x + 8.
3. HÀM SỐ ĐỒNG BIẾN, HÀM SỐ NGHỊCH BIẾN
Bài 1:
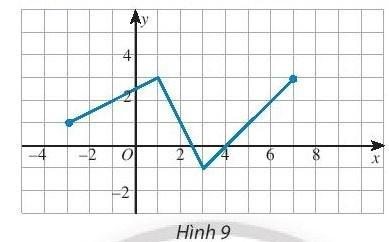
a) Tìm khoảng đồng biến và nghịch biến của hàm số có đồ thị sau:
b. Xét tính đồng biến, nghịch biến của hàm số y = f(x) = 5![]() trên khoảng (2; 5)
trên khoảng (2; 5)
Trả lời rút gọn:
a. Từ đồ thị, ta thấy hàm số xác định trên [-3; 7]
Trên khoảng (-3; 1), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (-3; 1).
Trên khoảng (1; 3), đồ thị có dạng đi xuống từ trái sang phải nên hàm số này nghịch biến trên khoảng (1; 3).
Trên khoảng (3; 7), đồ thị có dạng đi lên từ trái sang phải nên hàm số này đồng biến trên khoảng (3; 7).
b. Xét hàm số y = f(x) = 5![]() trên khoảng (2;5)
trên khoảng (2;5)
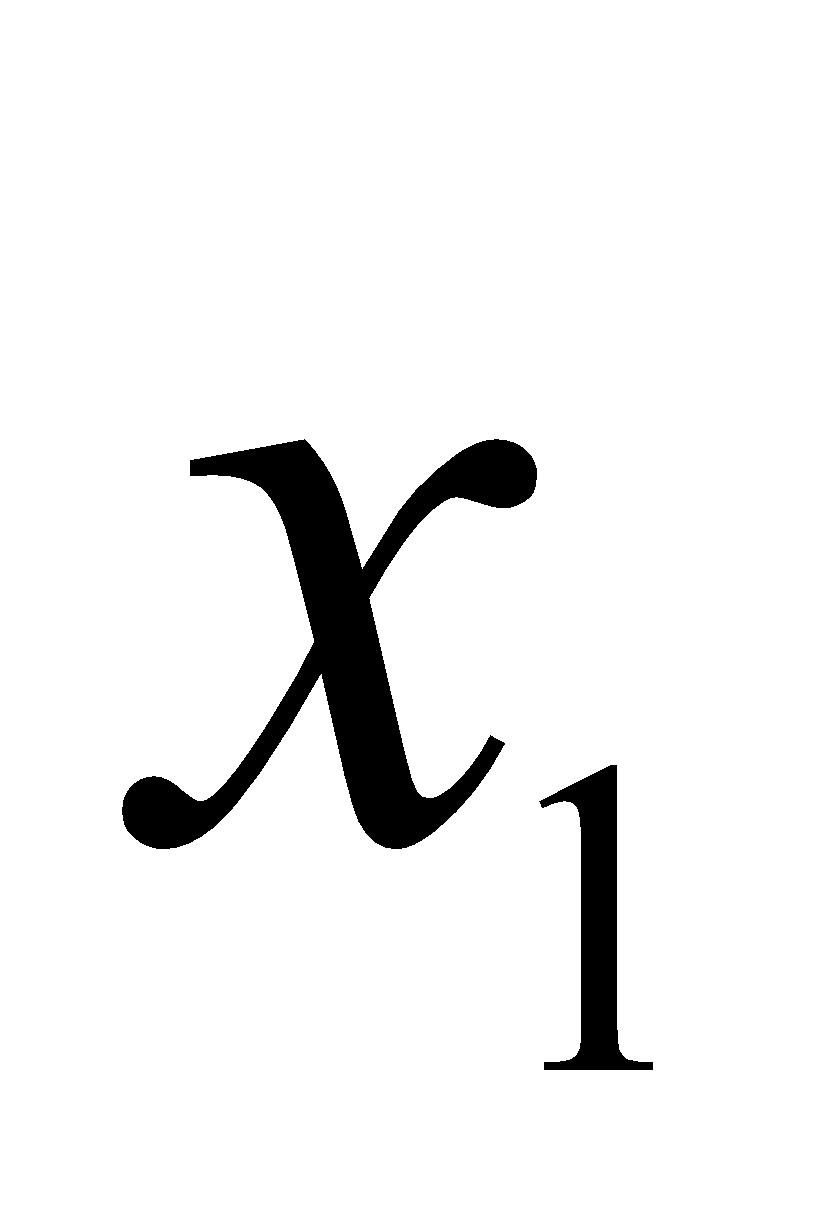 ,
, 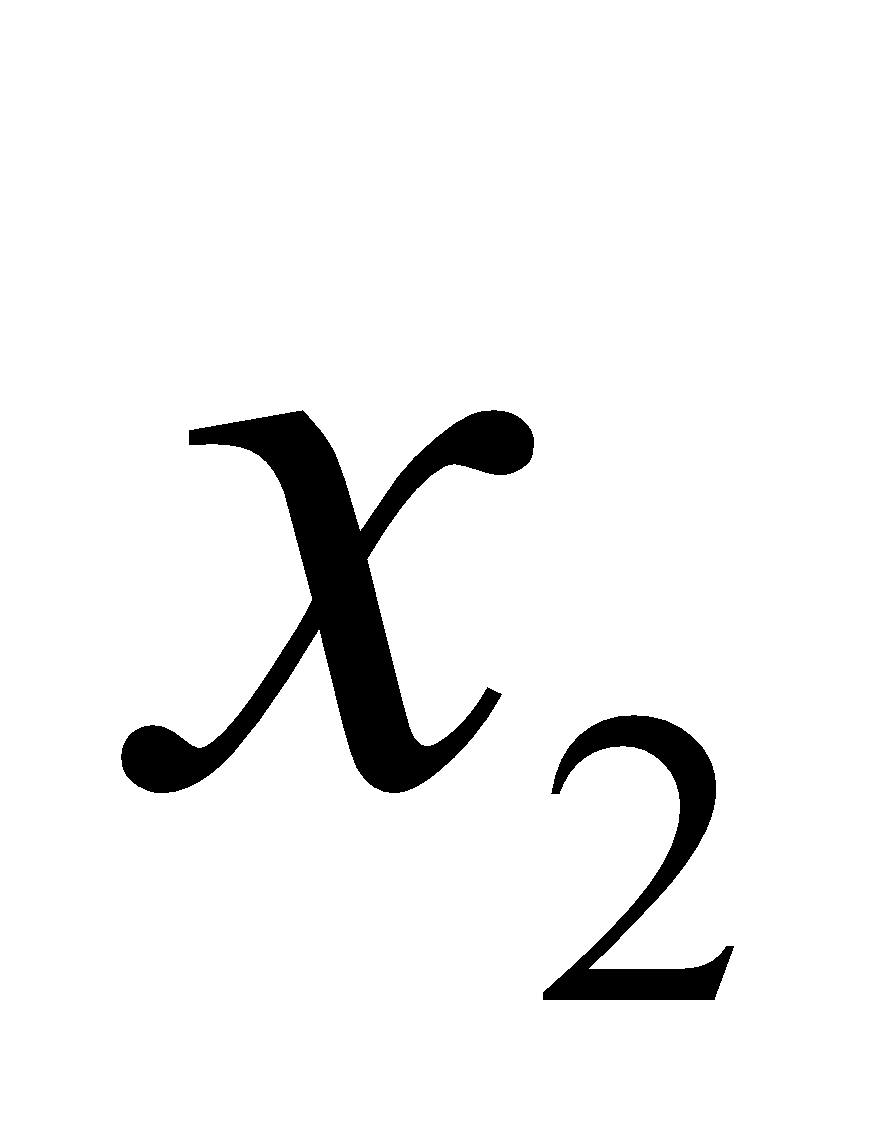 tùy ý sao cho
tùy ý sao cho 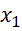 <
< 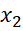 , có:
, có: f(
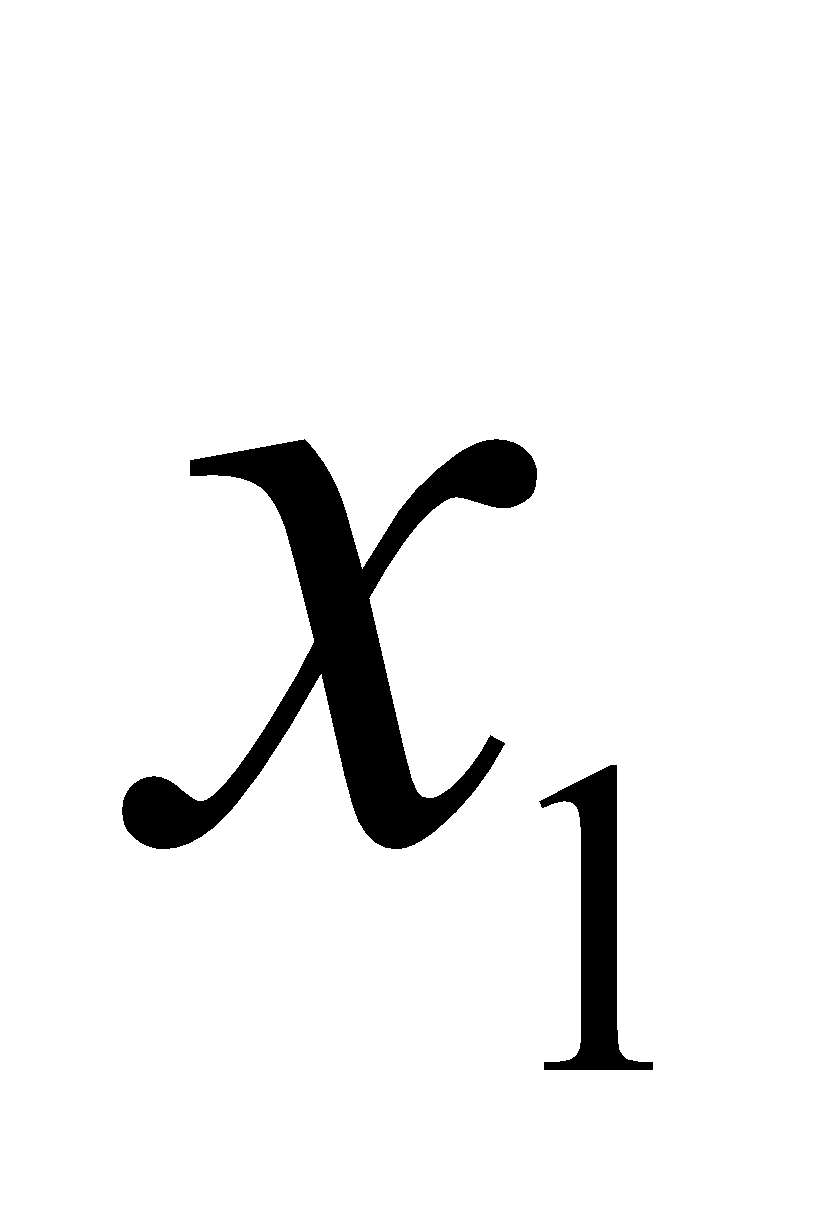 ) - f(
) - f(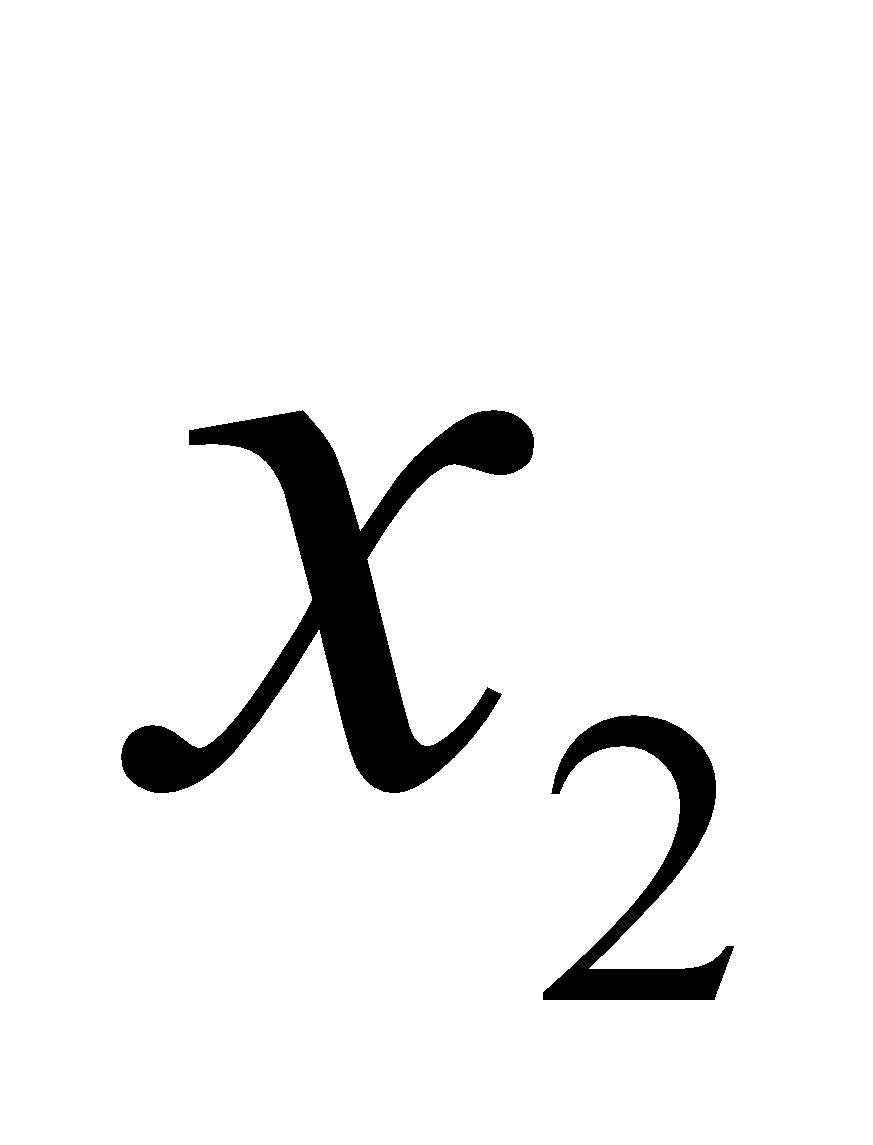 ) = 5(
) = 5(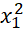 -
- 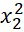 ) = 5(
) = 5(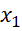 +
+ 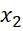 )(
)(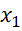 -
- 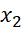 )
) 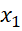 <
< 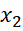 nên
nên 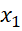 -
- 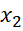 < 0
< 0 Do
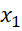 ,
, 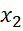
 (2; 5) nên (
(2; 5) nên (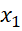 +
+ 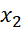 ) > 0. Từ đây suy ra f(
) > 0. Từ đây suy ra f(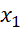 ) - f(
) - f(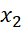 ) < 0 hay f(
) < 0 hay f(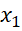 ) < f(
) < f(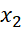 ).
).
Vậy hàm số đồng biến (tăng) trên khoảng (2; 5).
BÀI TẬP CUỐI SGK
Bài 1. Tìm tập xác định của các hàm số sau:
a. f(x) = ![]()
b. f(x) = ![]()
Trả lời rút gọn:
a) ![]()
![]() có nghĩa
có nghĩa ![]()
![]()
Vậy TXĐ của hàm số: ![]()
b) ![]()
![]() có nghĩa
có nghĩa ![]()
Vậy TXĐ của hàm số: ![]()
Bài 2. Tìm tập xác định, tập giá trị của hàm số có đồ thị như Hình 10.
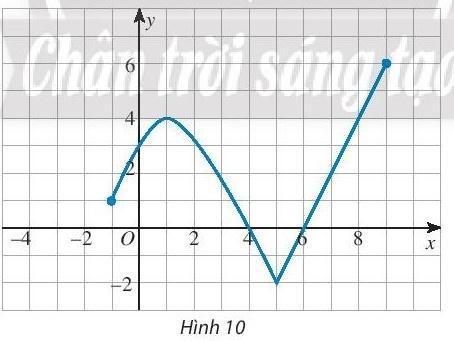
Trả lời rút gọn:
Tập xác định của hàm số là D = [-1; 9]
Tập giá trị của hàm số là T = [-2; 4]
Bài 3. Tìm các khoảng đồng biến, nghịch biến của các hàm số sau:
a. f(x) = -5x + 2 b. f(x) = -![]()
Trả lời rút gọn:
a. Xét hàm số y = f(x) = -5x + 2. Hàm số này xác định trên R.
Lấy ![]() ,
, ![]() là hai số tùy ý sao cho
là hai số tùy ý sao cho ![]() <
< ![]() ,có:
,có:
![]() <
< ![]()
![]() -5
-5![]() > -5
> -5![]()
![]() -5
-5![]() + 2 > -5
+ 2 > -5![]() + 2
+ 2 ![]() f(
f(![]() ) > f(
) > f(![]() ).
).
Vậy hàm số nghịch biến (giảm) / R
b. Xét hàm số f(x) = -![]() / R
/ R
![]() ,
, ![]() tùy ý sao cho
tùy ý sao cho ![]() <
< ![]() ,
,
Có f(![]() ) - f(
) - f(![]() ) = -
) = - ![]() +
+ ![]() = - (
= - (![]() -
- ![]() ) = - (
) = - (![]() +
+ ![]() )(
)(![]() -
- ![]() )
)
Do ![]() <
< ![]() nên
nên ![]() -
- ![]() < 0.
< 0.
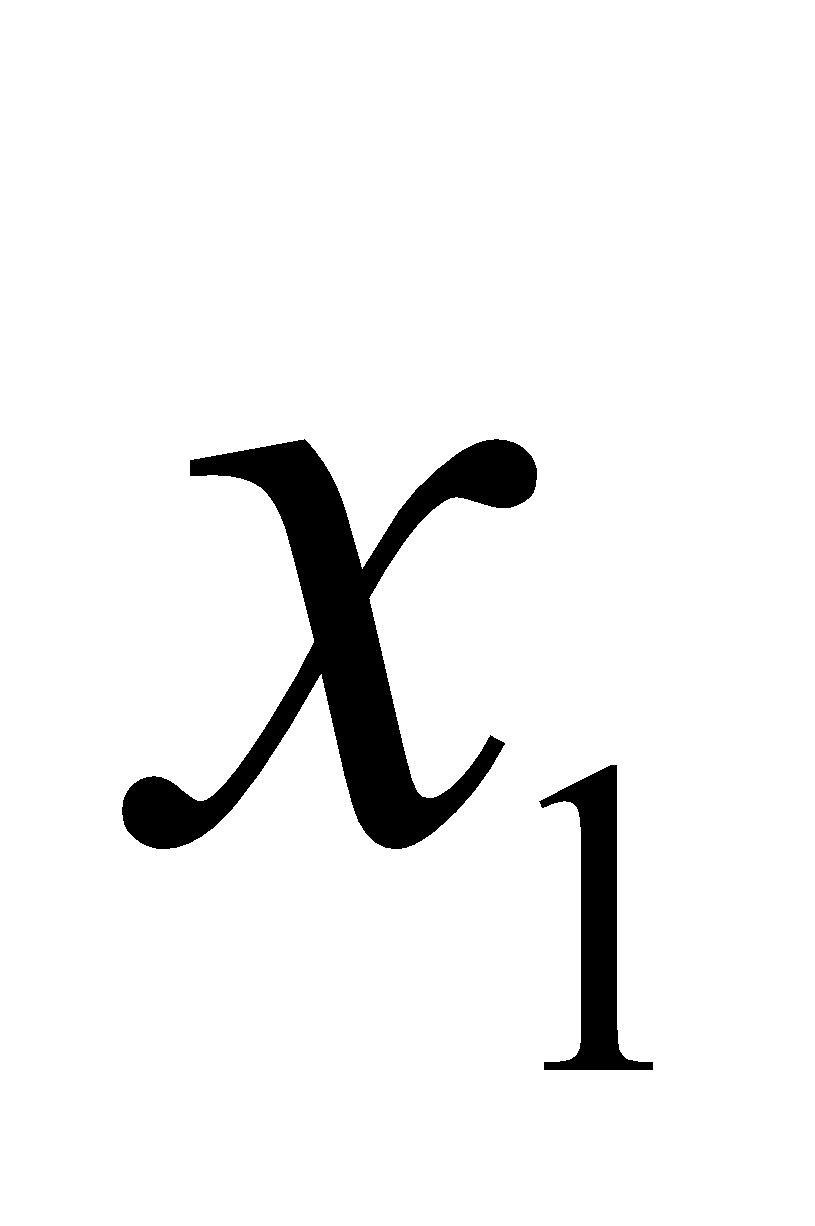 ,
, 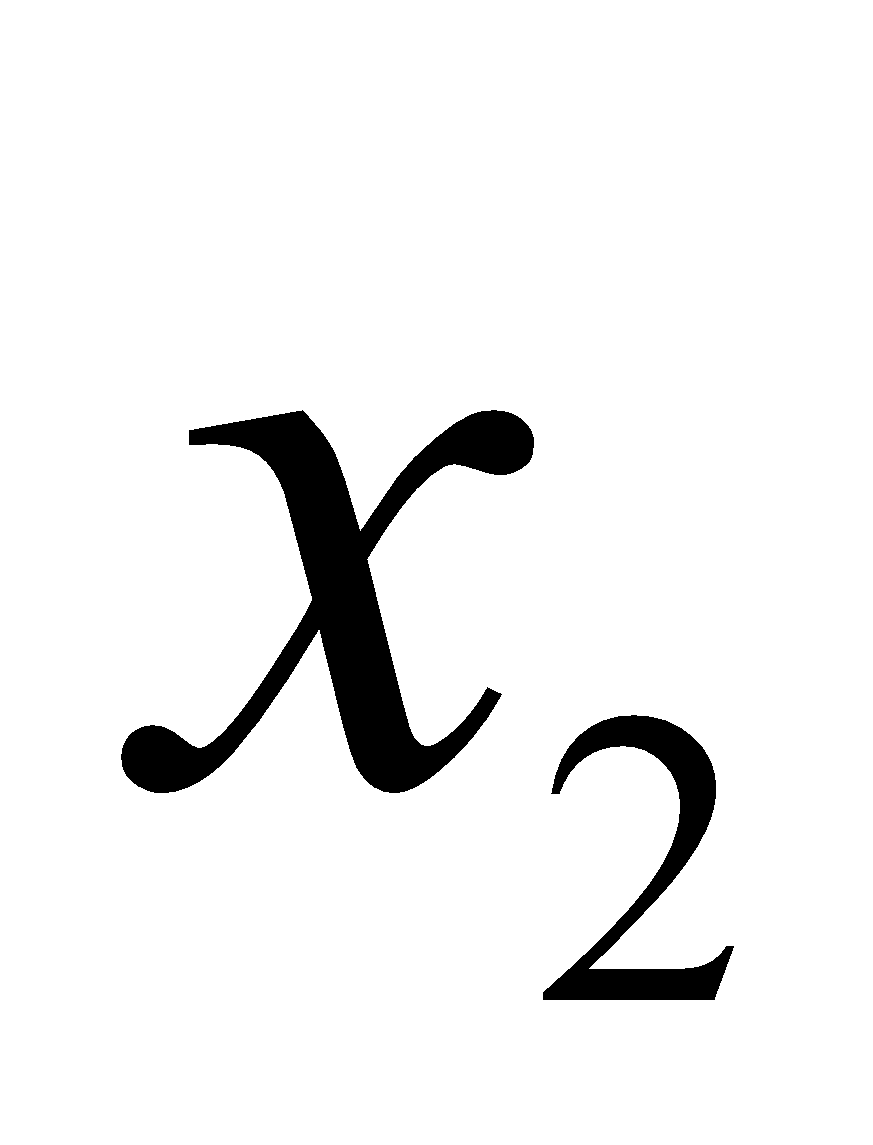
 (-
(- ; 0)
; 0) 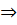
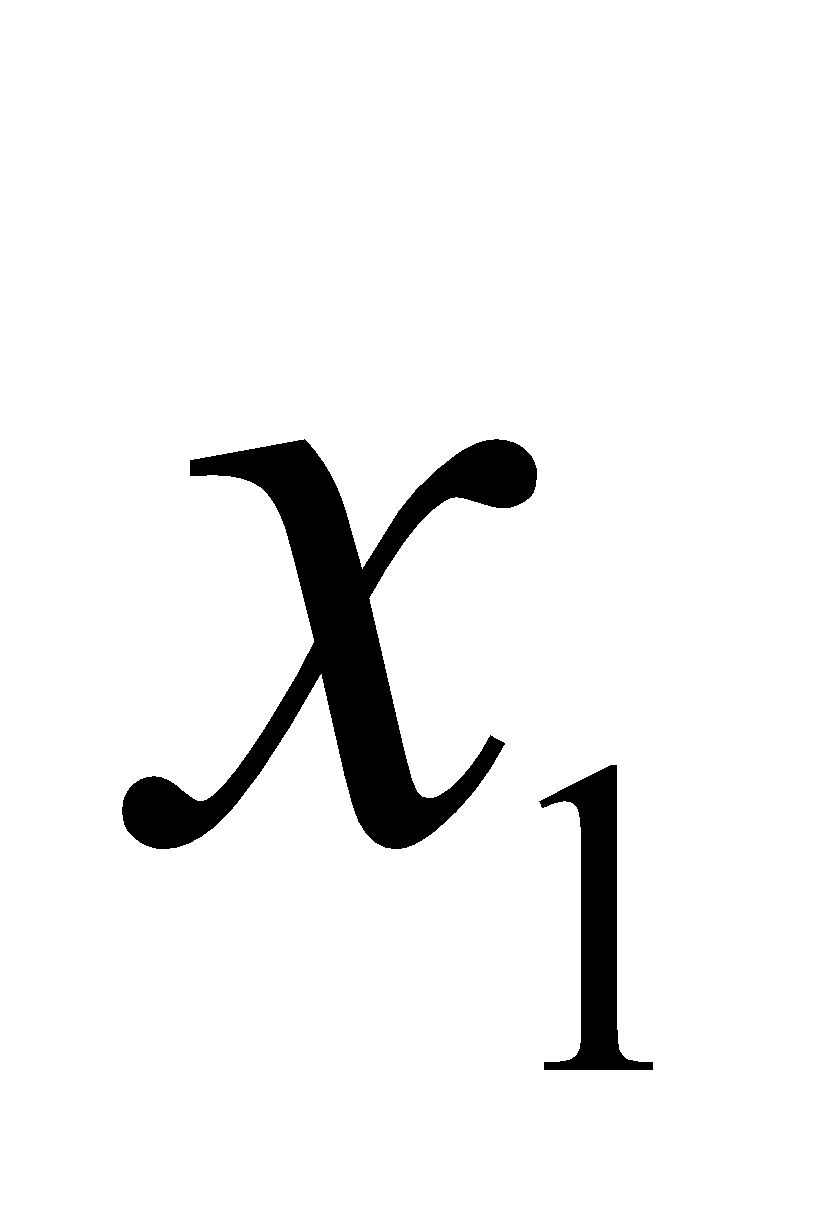 +
+ 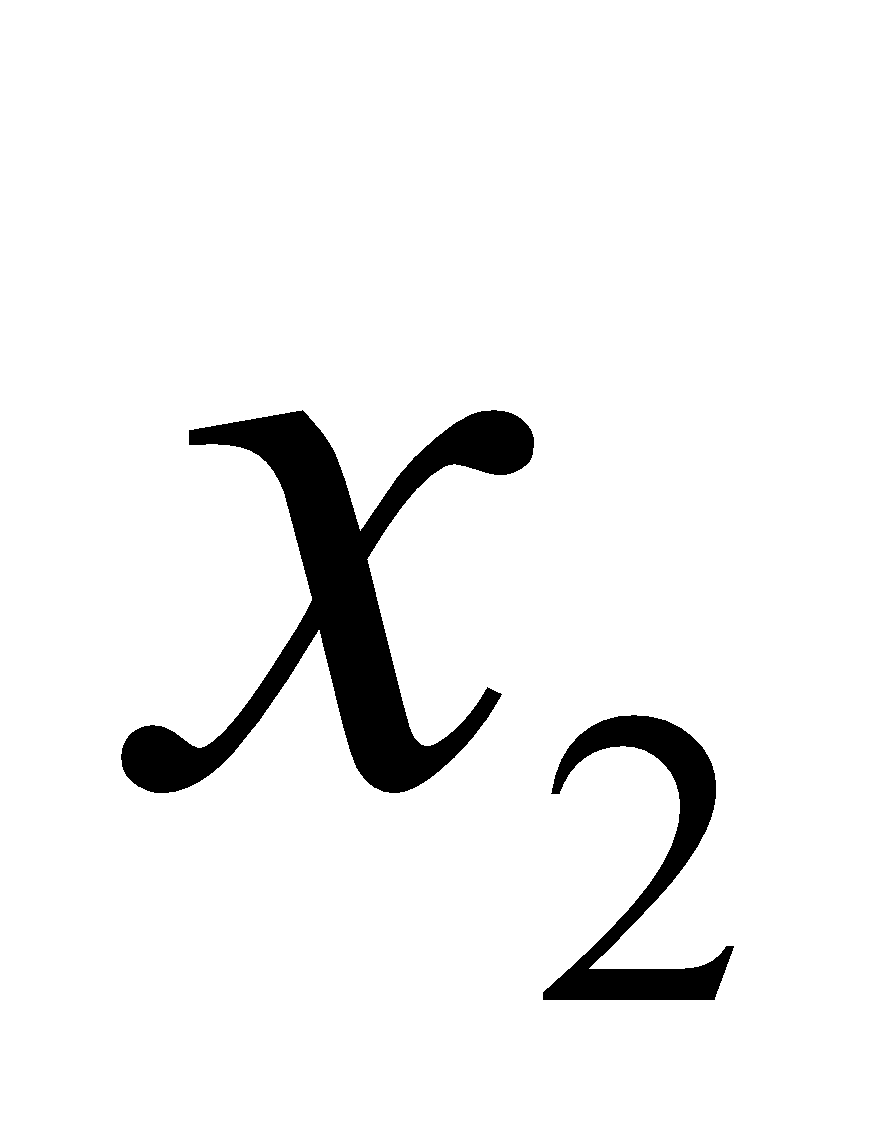 < 0
< 0 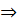 (
(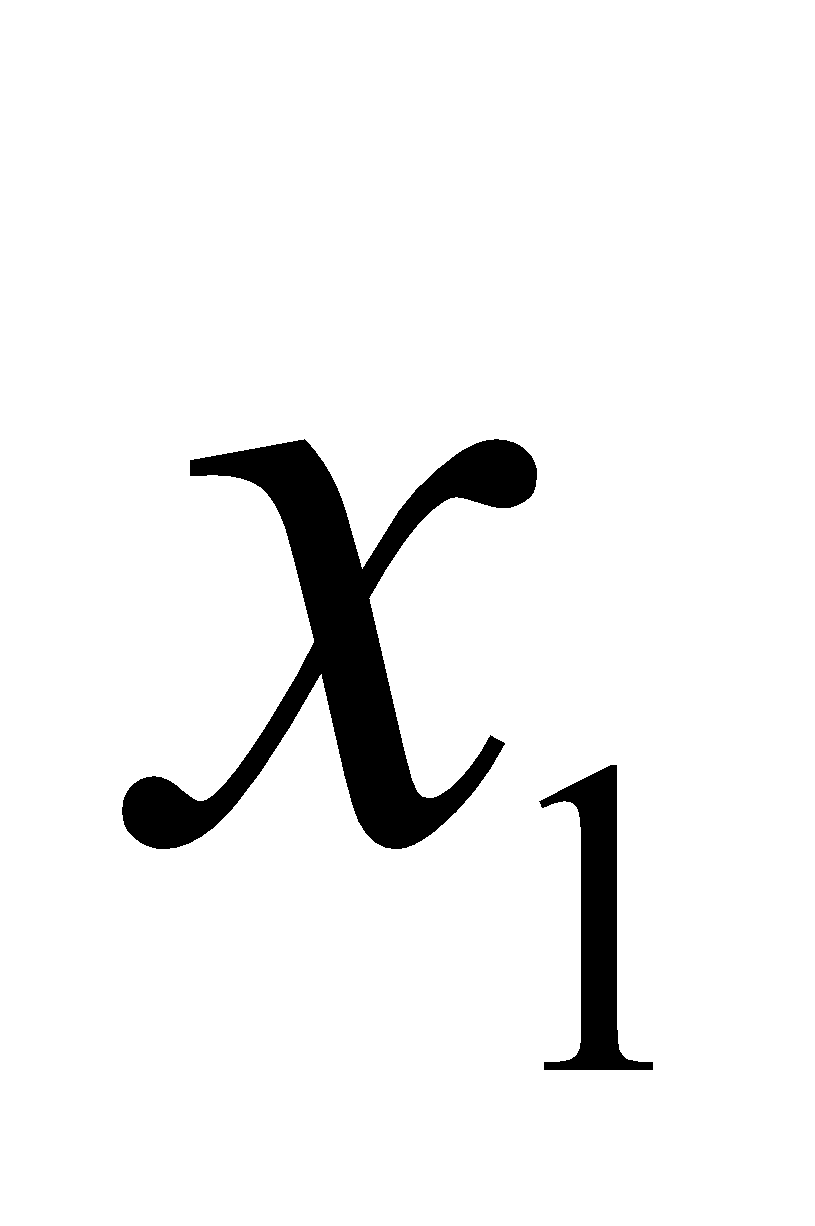 +
+ 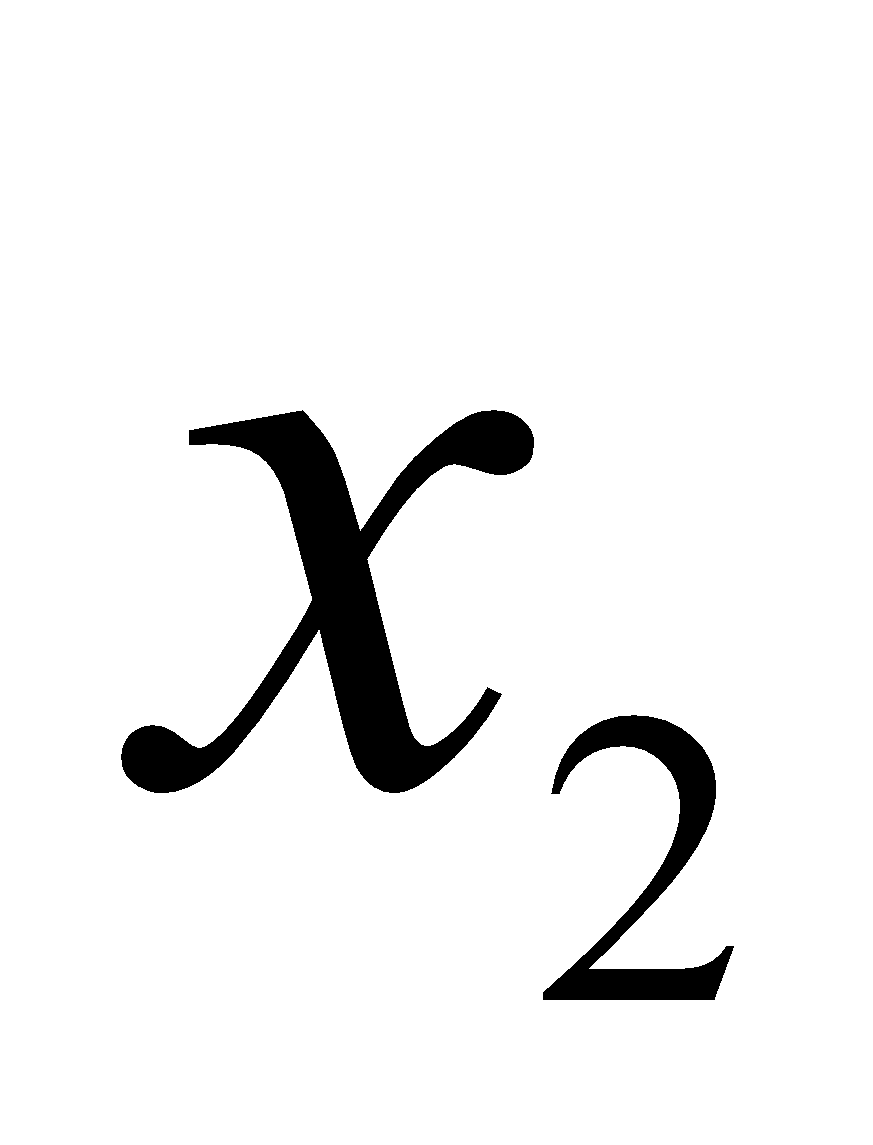 )(
)(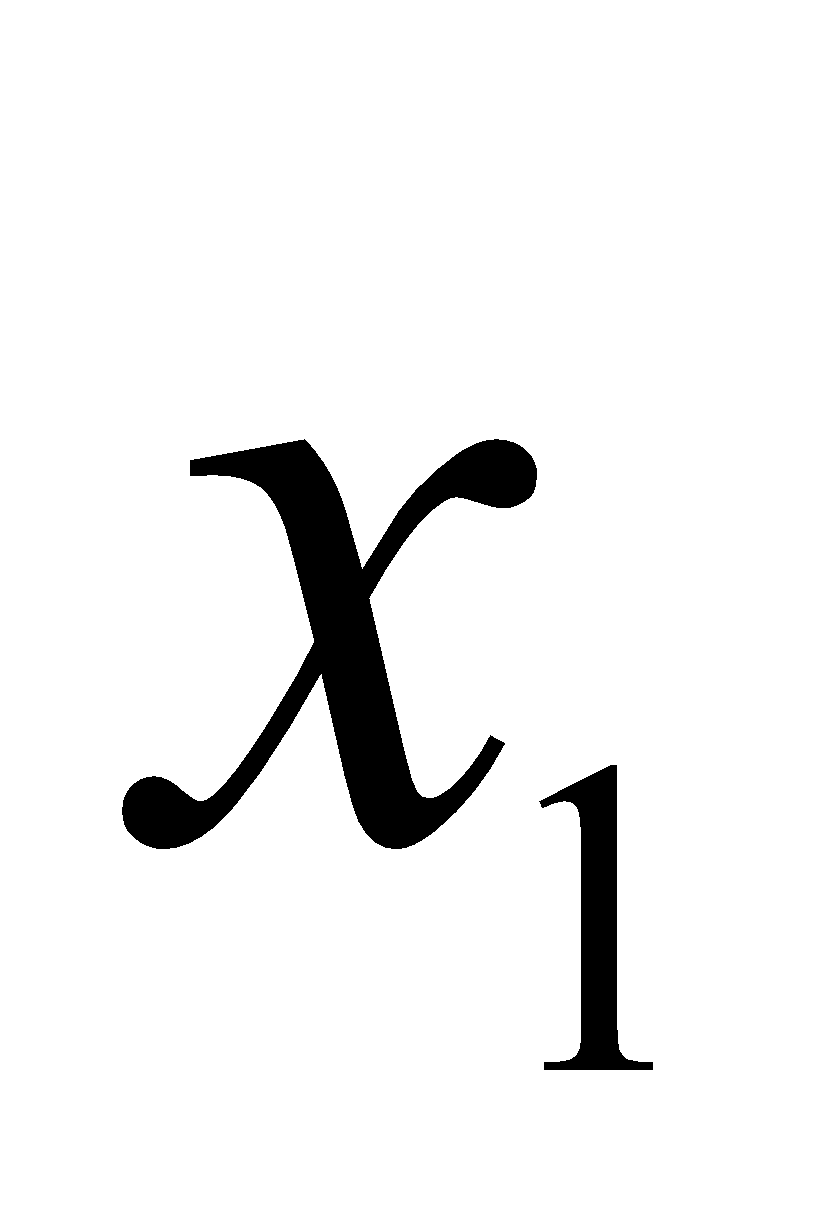 -
- 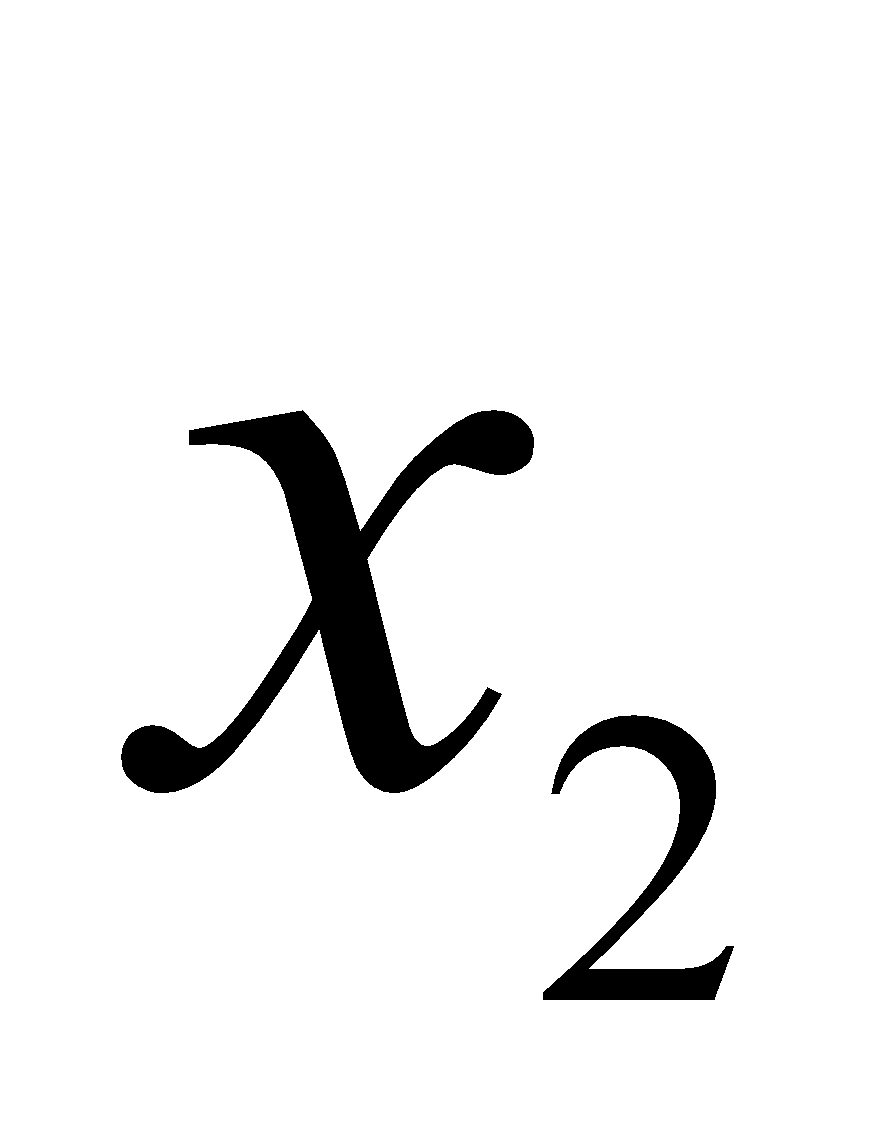 ) > 0
) > 0
![]() - (
- (![]() +
+ ![]() )(
)(![]() -
- ![]() ) < 0
) < 0 ![]() f(
f(![]() ) - f(
) - f(![]() ) < 0.
) < 0.
=> Hàm số đồng biến (tăng) /(-![]() ; 0).
; 0).
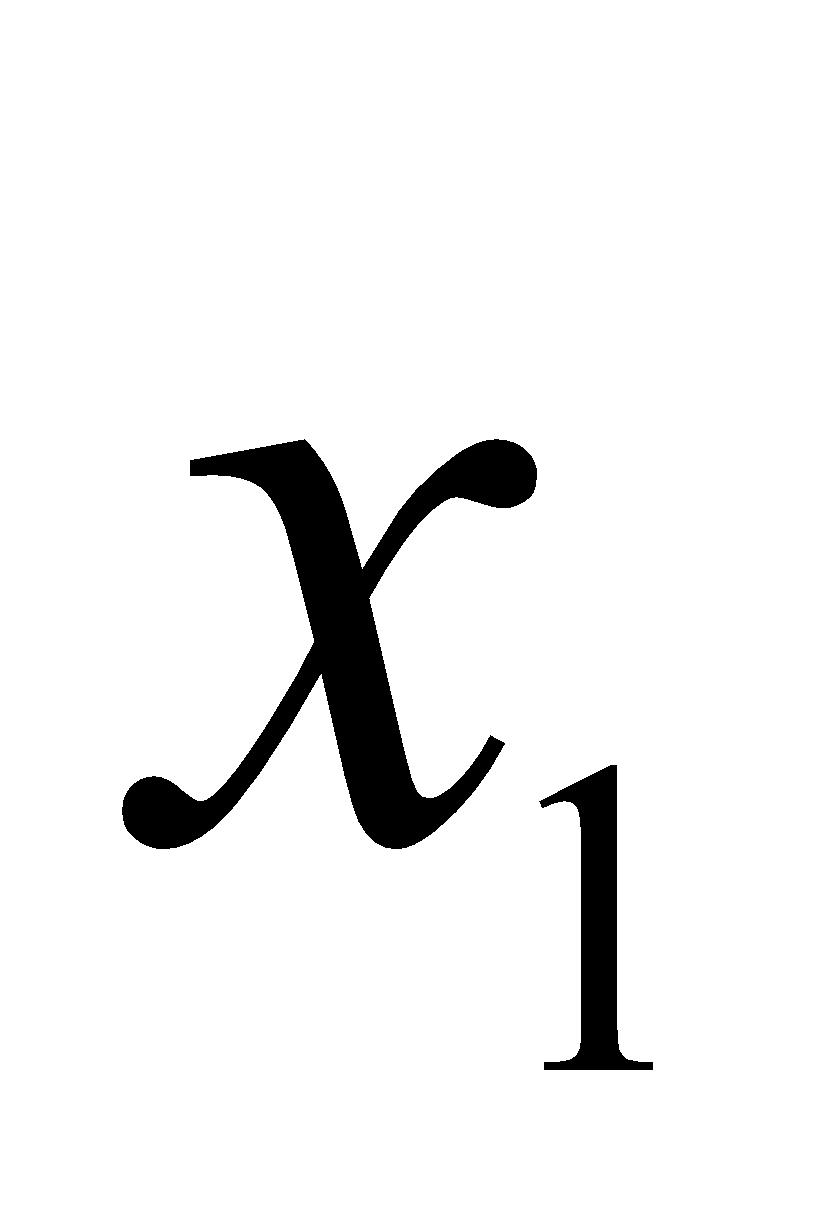 ,
, 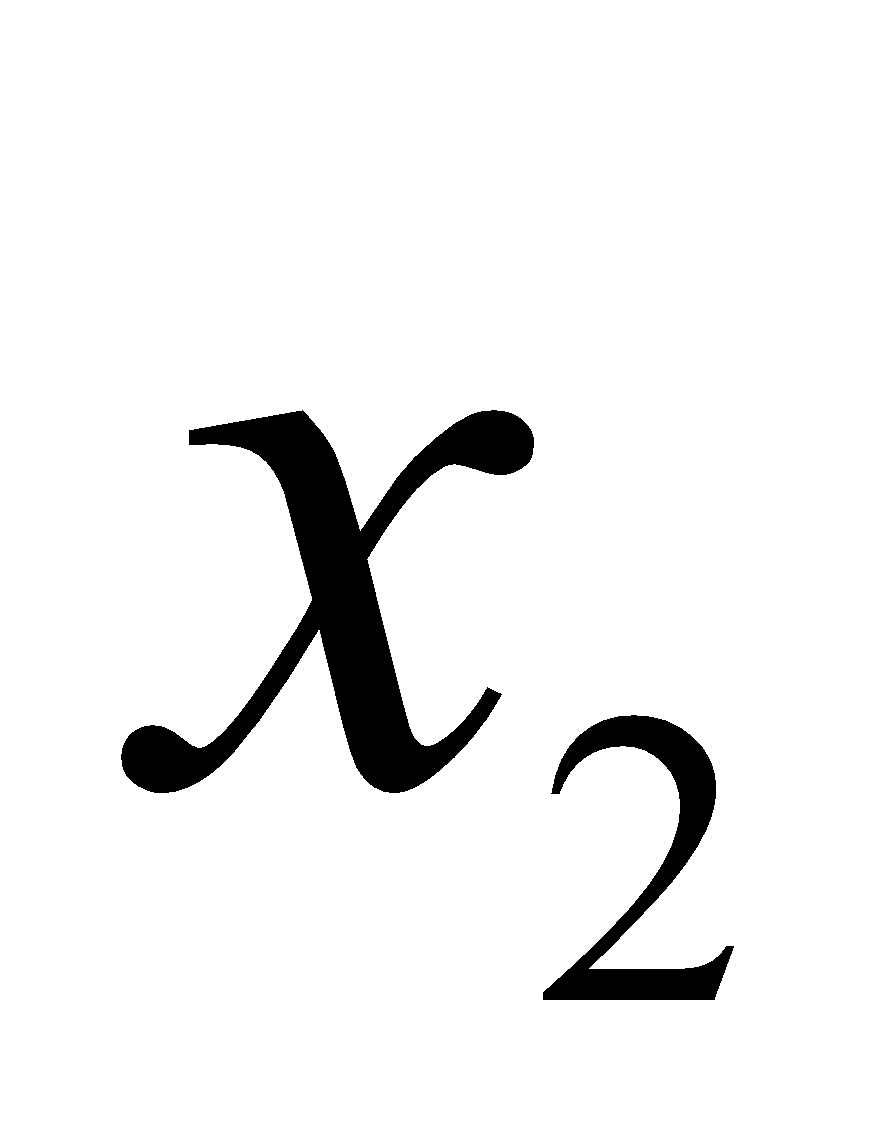
 (0; +
(0; + )
) 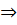
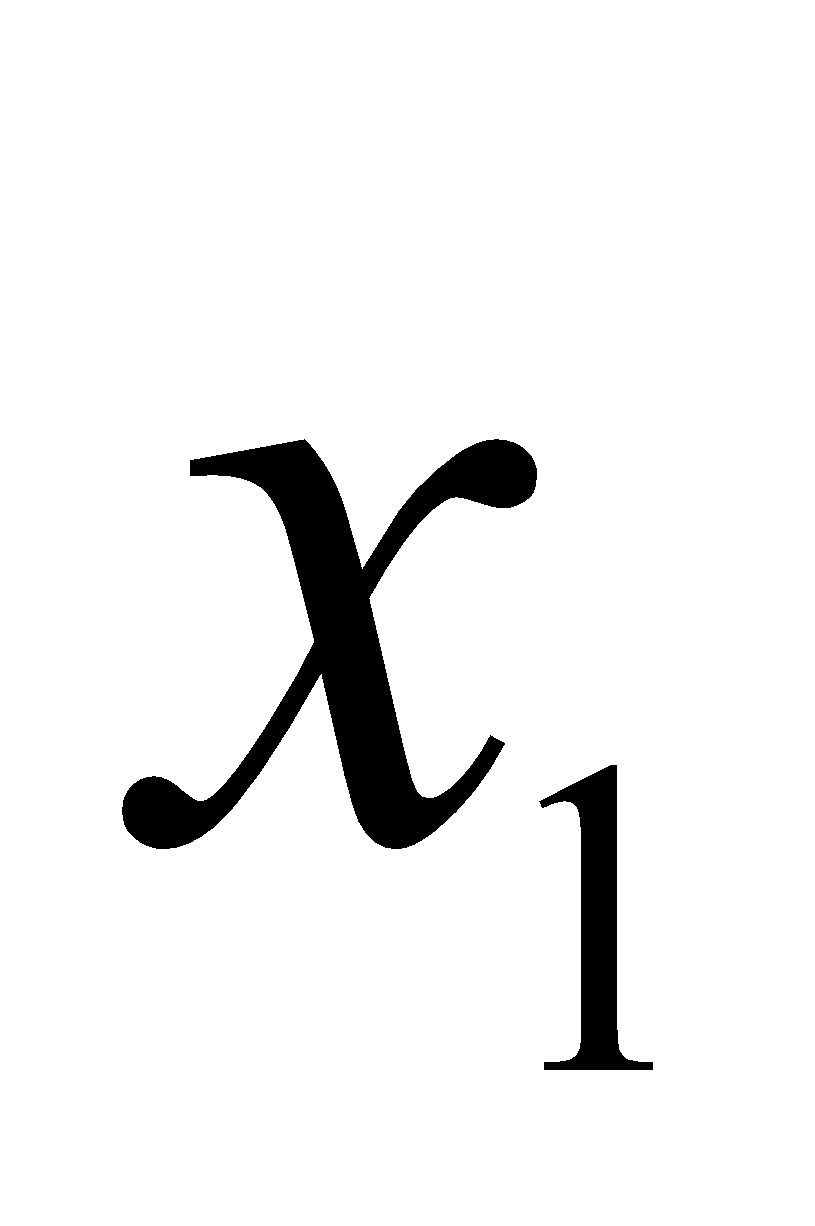 +
+ 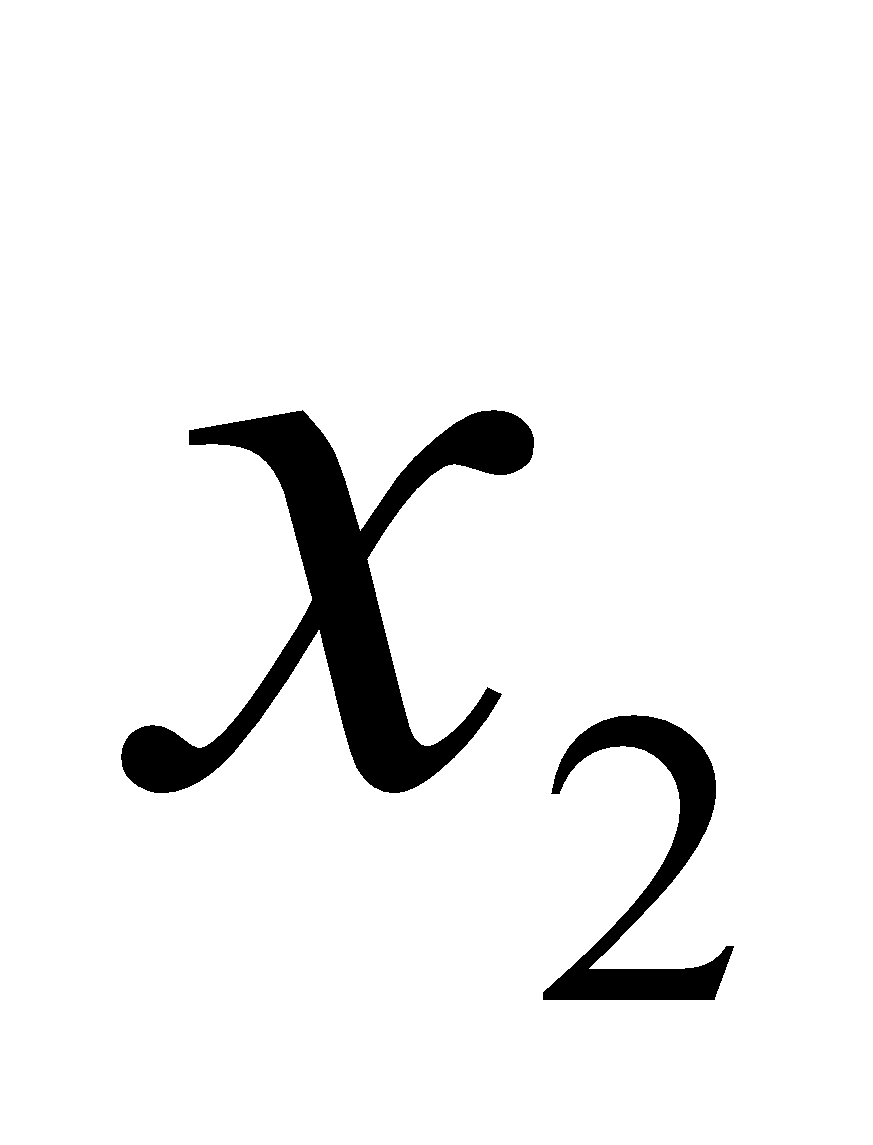 > 0
> 0 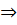 (
(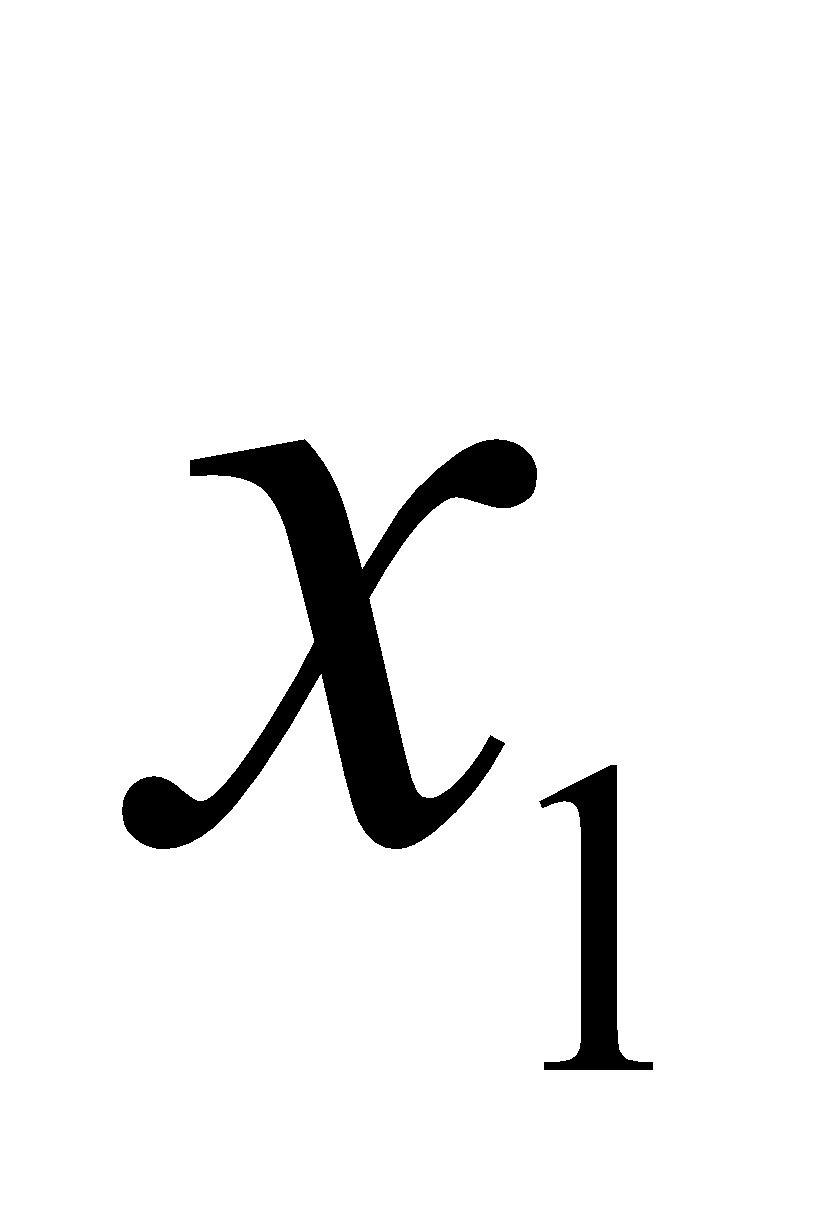 +
+ 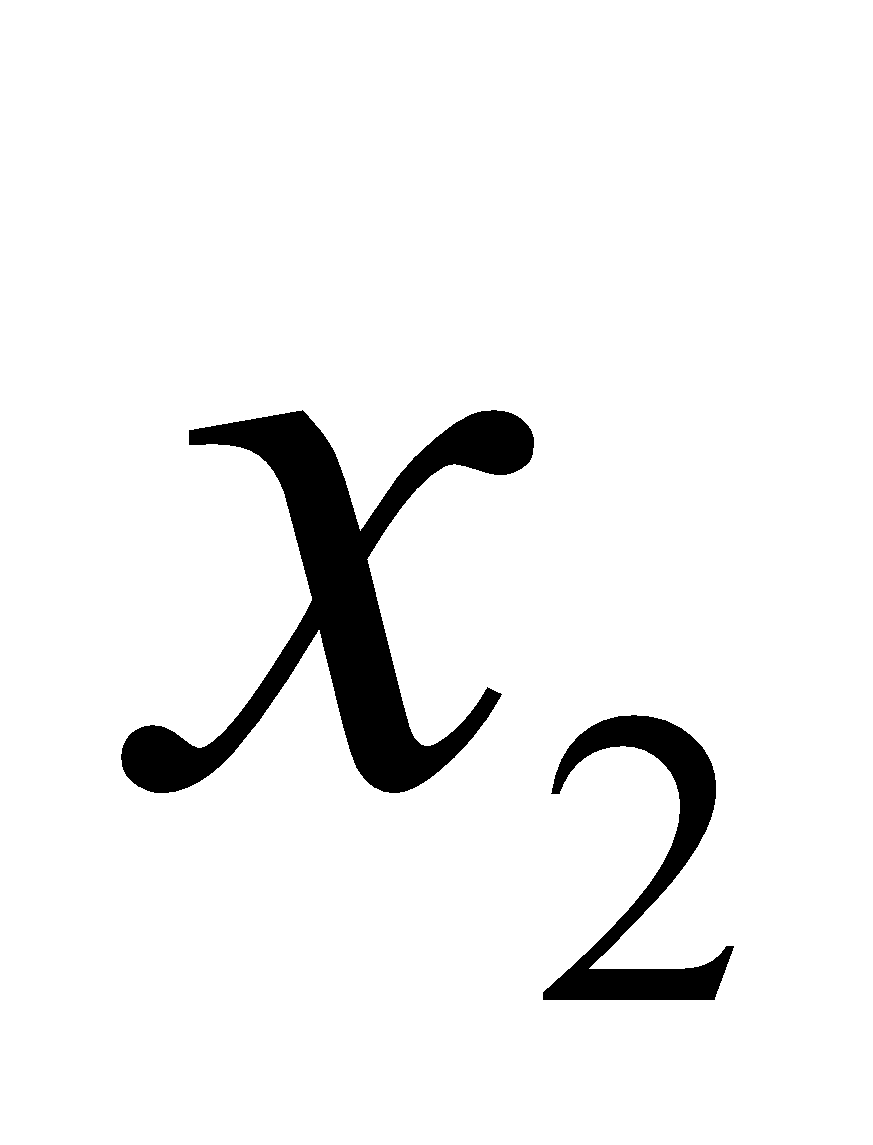 )(
)(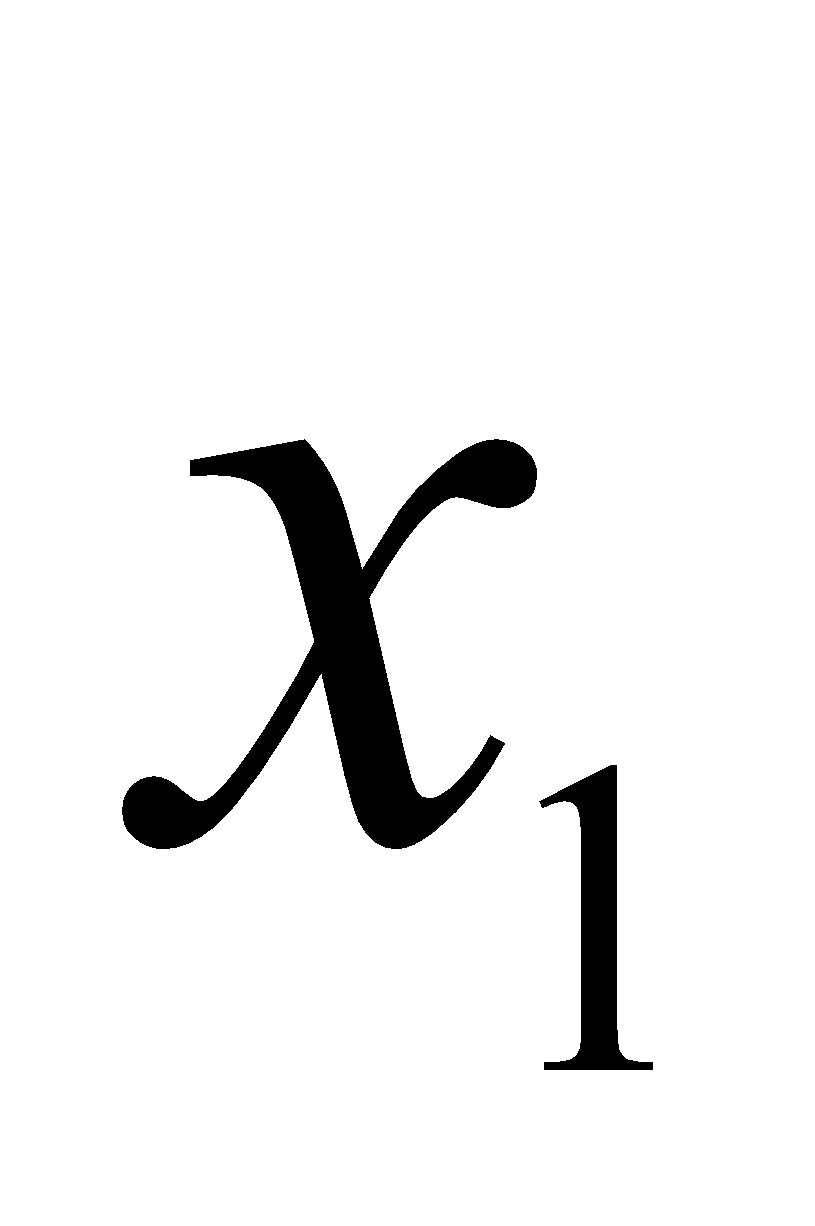 -
- 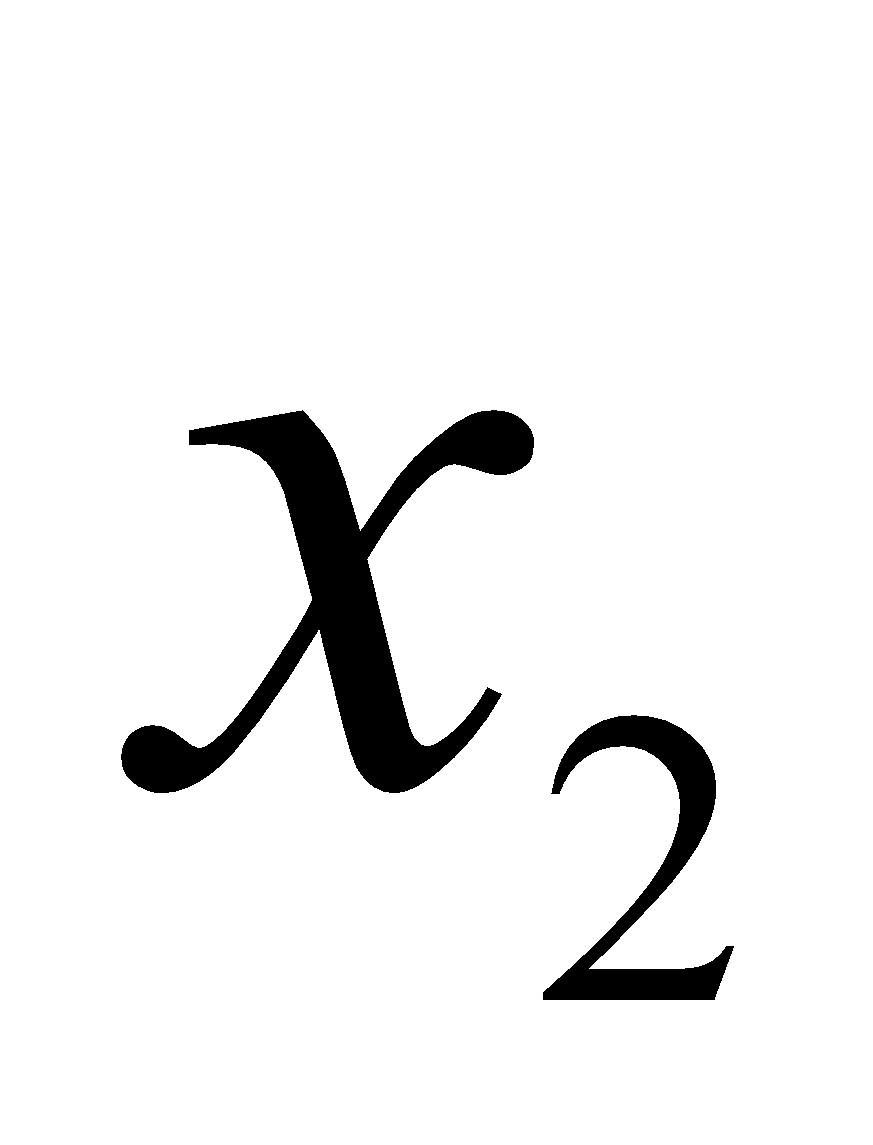 ) < 0
) < 0
=> - (![]() +
+ ![]() )(
)(![]() -
- ![]() ) > 0 => f(
) > 0 => f(![]() ) - f(
) - f(![]() ) > 0.
) > 0.
=> Hàm số nghịch biến (giảm) trên (0; +![]() ).
).
Vậy hàm số đồng biến (tăng) /(-![]() ; 0); hàm số nghịch biến (giảm) /(0; +
; 0); hàm số nghịch biến (giảm) /(0; +![]() )
)
Bài 4. Vẽ đồ thị hàm số f(x) = |x|, biết rằng hàm số này còn được viết như sau:
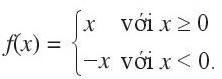
Trả lời rút gọn:
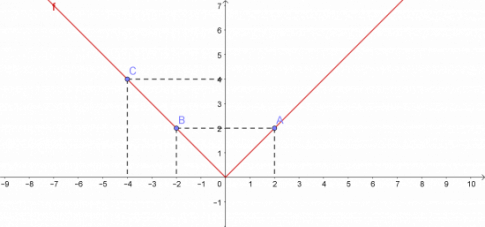
x ≥ 0, đồ thị y = x là đường thẳng đi qua điểm gốc tọa độ O(0; 0) và A(2; 2) nằm phía bên phải trục tung.
x < 0, đồ thị y = -x là đường thẳng đi qua hai điểm B(-2; 2) và C(-4; 4) nằm phía bên trái trục tung.
Bài 5. Tìm tập xác định, tập giá trị và vẽ đồ thị của hàm số:
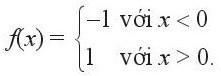
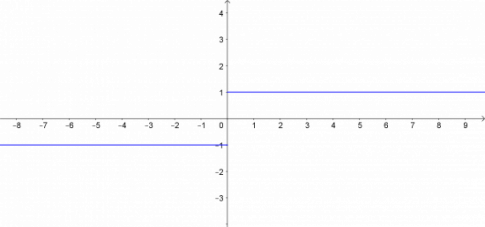
Trả lời rút gọn:
TXĐ của hàm số: D = R\{0}
TGT của hàm số: T = {-1; 1}
x < 0, đồ thị y = f(x) là đường thẳng y = -1 // Ox và nằm bên trái trục tung.
x > 0, đồ thị y = f(x) là đường thẳng y = 1 // Ox và nằm bên phải trục tung.
Bài 6. Một hãng taxi có bảng giá như sau:
| Giá mở cửa (0,5 km) | Giá cước các km tiếp theo | Giá cước từ km thứ 31 |
Taxi 4 chỗ | 11 000 đồng | 14 500 đồng | 11 600 đồng |
Taxi 7 chỗ | 11 000 đồng | 15 500 đồng | 13 600 đồng |
a. Xem số tiền đi taxi là một hàm số phụ thuộc vào số kilomet di chuyển, hãy viết công thức của các hàm số dựa trên thông tin từ bảng giá đã cho theo từng yêu cầu:
Hàm số f(x) để tính số tiền hành khách phải trả khi di chuyển bằng x km bằng xe taxi 4 chỗ.
Hàm số g(x) để tính số tiền hành khách phải trả khi di chuyển x km bằng xe taxi 7 chỗ.
b. Nếu cần đặt xe taxi cho 30 hành khách, nên đặt toàn bộ xe 4 chỗ hay xe 7 chỗ thì có lợi hơn?
Trả lời rút gọn:
a.
|
|
|
|
b. Có: 30 = 4.7 + 2
=> Nếu cần đặt taxi cho 30 hành khách, cần ít nhất 8 xe 4 chỗ và 5 xe 7 chỗ.
Số tiền phải trả nếu thuê toàn bộ xe 4 chỗ là :
8. [11 000 + 14 500. 31 + 11 600(x - 31)] = 807 500 + 92 800. x (1)
Số tiền phải trả nếu thuê toàn bộ xe 7 chỗ là :
5. [11 000 + 15 500. 31 + 13 600(x - 31)] = 349 500 + 68 000. x (2)
Từ (1) và (2) => đặt toàn bộ xe 7 chỗ sẽ có lợi hơn.
Bài 7. Đố vui
Số 2 đã trải qua một hành trình thú vị và bị biến đổi sau khi đi qua chiếc hộp đen.

Bác thợ máy đã giải mã hộp đen cho một số x bất kì như sau:
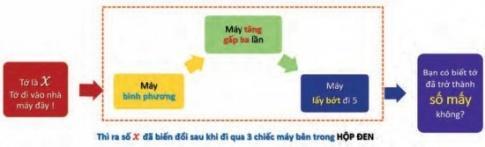
Bên trong HỘP ĐEN là một đoạn chương trình được cài đặt sẵn. Ta xem đoạn chương trình này như một hàm số f(x). Hãy viết biểu thức của f(x) để mô tả sự biến đổi đã tác động lên x.
Trả lời rút gọn:
Số x đi qua máy bình phương thì biến đổi thành x2.
x2 đi qua máy tăng gấp ba lần thì biến đổi thành 3x2
3x2 đi qua máy lấy bớt đi 5 thì biến đổi thành 3x2 – 5.
=> Vậy f(x) = 3x2 – 5.
