Slide bài giảng toán 10 chân trời bài 1: Dấu của tam thức bậc hai

Tóm lược nội dung

BÀI 1. DẤU CỦA TAM THỨC BẬC HAI

KHỞI ĐỘNG

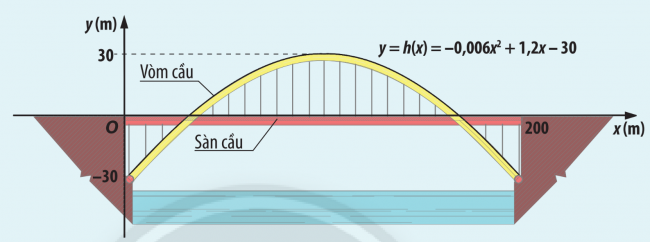
Cầu vòm được thiết kế với thanh vòm hình Parabol và mặt cầu ở đi ở giữa. Trong hệ trục tọa độ Oxy như hình vẽ, phương trình của vòm cầu 

y = h(x) = −0,006+1,2x−30. Với giá trị h(x) như thế nào tại vị trí x(0≤x≤200), vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu?

Trả lời rút gọn: 

• Giá trị h (x) > 0 -> vòm cầu cao hơn mặt cầu

• Giá trị h (x) < 0 -> vòm cầu thấp hơn mặt cầu.

1. TAM THỨC BẬC HAI

Bài 1: Đồ thị của hàm số y = f(x) = − +x+3 được biểu diễn trong Hình 1.

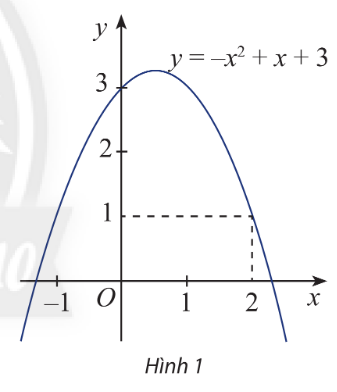
a. Biểu thức f(x) là đa thức bậc mấy?

b. Xác định dấu của f(2).

Trả lời rút gọn: 

a. Biểu thức f(x) là đa thức bậc hai.

b. Có: f(2)=− 2²+2+3=1 > 0

=> f(2) mang dấu dương.

Bài 2. Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét dấu của nó tại x = 1.

a.  f(x) = −2+x−1

b.  g(x) = −+2+1

c. h(x) = −+x−3

Trả lời rút gọn: 

Bài 3: Tìm biệt thức và nghiệm của tam thức bậc hai sau:

a. y=f(x)=2−5x+2

b. y=g(x)=− +6x−9

c. y=h(x)=4−6x+9

Trả lời rút gọn: 

2. ĐỊNH LÍ VỀ DẤU CỦA TAM THỨC BẬC HAI

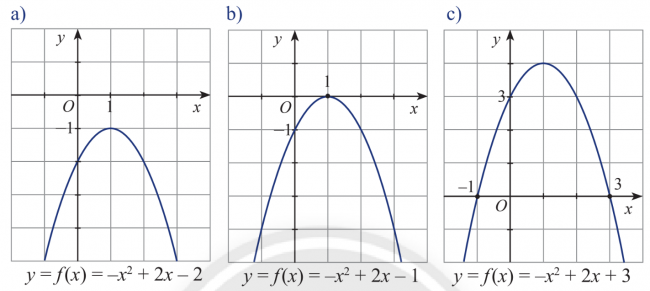
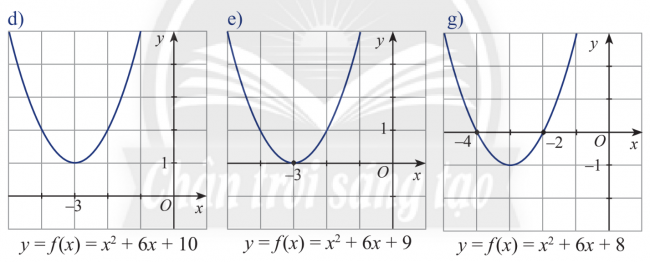
Bài 1: Quan sát đồ thị của các hàm số bậc hai trong các hình dưới đây. Trong mỗi trường hợp, hãy cho biết:

Các nghiệm (nếu có) và dấu của biệt thức Δ.

Các khoảng giá trị của x mà trên đó f(x) cùng dấu với hệ số của x².

Trả lời rút gọn: 

Bài 2: Xét dấu của các tam thức bậc hai:

a. f(x)=2−3x−2 

b. g(x)=− +2x−3

Trả lời rút gọn: 

a. f(x)=2−3x−2 

 Δ=25 > 0

=> hai nghiệm phân biệt:  x₁ = và x₂ = -2.

Bảng xét dấu f(x):

Vậy f(x) dương trong khoảng (−∞;  −12 ) ∪ (−12 ; +∞ ) và âm trong khoảng (− ; 2). 

b. g(x)=− +2x−3 có: Δ=−8 < 0 và a = -1 < 0.

Vậy g(x) âm với mọi x∈R.

Bài 3: Xét dấu của tam thức bậc hai h(x)=−0,006+1,2x−30 trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu.

Trả lời rút gọn: 

y=h(x)=−0,006+1,2x−30  có: Δ= > 0 hai nghiệm phân biệt là:

x₁ =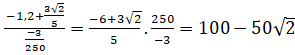

x₂ =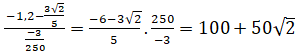

Bảng xét dấu f(x):

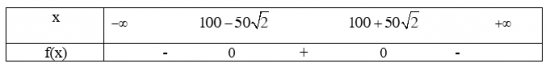
Vòm cầu cao hơn mặt cầu khi x∈(100−;100+) 

thấp hơn mặt cầu khi x∈(−∞;100−)∪(100+;+∞)

BÀI TẬP CUỐI SGK

Bài 1. Đa thức nào sau đây là tam thức bậc hai?

a. 4+3x+1

b. +3−1

c. 2+4x−1

Trả lời rút gọn: 

Bài 2. Xác định giá trị của m để các đa thức sau là tam thức bậc hai.

a. (m+1)+2x+m

b. m+2−x+m

c. −5+2x−m+1

Trả lời rút gọn: 

Bài 3. Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

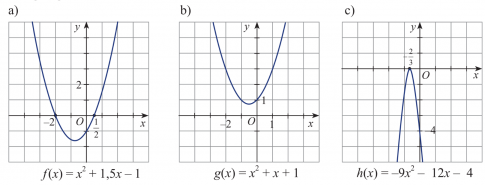
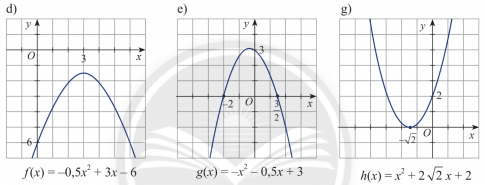
Trả lời rút gọn: 

a. f(x)= +1,5x−1 có Δ=>0 , hai nghiệm phân biệt 

  x₁=−2 ; x₂= và a = 1 > 0

Bảng xét dấu f(x):

Vậy f(x) dương trong hai khoảng (−∞;) và (−2;+∞) và âm trong khoảng (;−2). 

b. g(x)=x²+x+1 có Δ=−3<0 và a =1 >0 . 

=> f(x) dương với mọi x∈R

c. h(x)=−9x²−12x−4 có  Δ=0, nghiệm kép 

 x_o= và a = -9  < 0.

=> f(x) âm với mọi x ≠

d. f(x)=−0,5x²+3x−6 có Δ= −3<0 và a =-0,5 

=> f(x) âm với mọi x∈R

e. g(x)=−x²−0,5x+3 có Δ=  > 0 , hai nghiệm phân biệt 

 x₁=−2 ; x₂= và a = -1 < 0

Ta có bảng xét dấu f(x) như sau:

=> f(x) dương trong hai khoảng (−∞;−2) và (;+∞) và âm trong khoảng (−2; ).

g. h(x)=x²+2x+2 có  Δ=0, nghiệm kép là xo=− và a = -9 < 0.

=> f(x) âm với mọi x≠-

Bài 4. Xét dấu của tam thức bậc hai sau đây

a. f(x) = 2x²+4x+2

b. f(x) = -x²+2x+21

c. f(x) = −2x²+x−2

d. f(x) = −4x(x+3)−9

e. f(x) = (2x+5)(x−3)

Trả lời rút gọn: 

a. Δ = 4² - 4.2.2 = 0. => x= = -1

a= 2 > 0 => f(x) luôn dương ∀x ≠ -1

b. Δ = 2² - 4(-3).21 = 256 > 0 nên phương trình có hai nghiệm phân biệt : x= và a= -1 < 0 

=> f(x) mang dấu âm khi x ∈ (; 3) và mang dấu dương ∀x ∈ (; 3)

c. Δ = (−2)² - 4(-2)(-2)= -12< 0 và a= -2 < 0 

=> f(x) luôn âm ∀x

d. f(x)= -4x² - 12x -9.

Δ = (−12)² - 4(-4)(-9) = 0 nên có nghiệm kép là x = -1,5 và a= -4

⇒ f(x) mang dấu âm với ∀x ≠ -1,5

e. f(x) = 2x² - x - 15. 

Δ = (−1)² - 4.2.15= -119 < 0, a= 2 > 0 

=> f(x) luôn mang dấu dương ∀x

Bài 5. Độ cao ( tính bằng mét) của quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng theo hàm số h(x) = −0,1x²+x−1. Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ, và ngang vành rổ. Làm tròn kết quả đến hàng phần mười. 

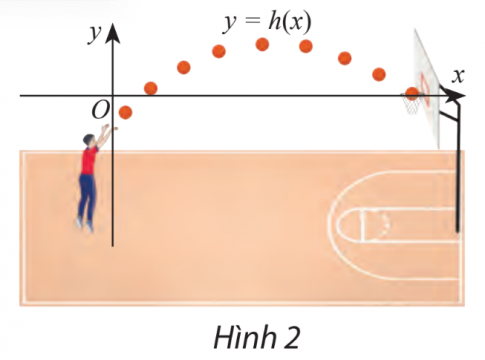
Trả lời rút gọn: 

h(x) có Δ = 1² -4(-0,1)(-1) = 0,6 >0 có hai nghiệm phân biệt :

 x₁ = 9, x₂ = 1. và a = -0,1<0

Vậy :

• Bóng nằm cao hơn vành rổ khi bóng nằm ∈ (1;9)

• Bóng nằm thấp hơn vành rổ khi bóng nằm ∈ (-∞; 1) và ( 9; +∞)

• Bóng nằm ngang vành rổ khi bóng ở độ cao 1m hoặc 9m

Bài 6. Một khung dây thép hình chữ nhật có chiều dài 20cm và chiều rộng 15cm được uốn lại thành khung hình chữ nhật mới có kích thước (20+x) và (15−x) cm. Với x nằm trong khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi. 

Trả lời rút gọn: 

Diện tích khung dây thép chưa uốn : 20.15 = 300 (cm²)

Diện tích khung dây thép đã uốn : (20+x).(15−x)=300−5x−x². 

=> Diện tích của khung sau khi uốn tùy thuộc vào giá trị của f(x) =  5x+x². 

f(x) có Δ = 5² - 4.1.0 = 25 > 0 ⇒ hai nghiệm phân biệt :

x₁ = ; x₂ = = 0 , có a = 1 > 0. 

• f(x) mang dấu dương khi x ∈ (-5;0) ⇒ Diện tích khung hình sau khi uốn nhỏ hơn trước khi uốn (giảm đi )

• f(x) mang dấu âm khi x ∈ (-∞; -5) và (0 ; +∞) ⇒ Diện tích khung hình sau khi uốn lớn hơn trước khi uốn (tăng lên )

• f(x) = 0 khi x = 0 hoặc x = -5 ⇒ Diện tích khung hình sau khi uốn và trước khi uốn là không thay đổi

Bài 7. Chứng minh rằng với mọi số thực m ta luôn có : 9m²+2m>−3

Trả lời rút gọn: 

Xét hàm số f(m) =  9m²+2m+3. Δ = 2²−4.9.3=−104 < 0 , a = 9>0

=> f(m) > 0 ∀ m:  9m²+2m>3

Bài 8. Tìm giá trị của m để :

a. 2x²+3x+m+1>0 với mọi x ϵ R

b. mx²+5x−3 ≤ 0 với mọi x ϵ R

Trả lời rút gọn: 

a. Hàm số 2x²+3x+m+1 có Δ = 3²−4.2(m+1)=1−8m. a= 2 > 0

 2x²+3x+m+1>0 ∀ x ϵ R thì Δ < 0 ⇒ 1−8m<0 ⇒ m>18

b. Hàm số mx²+5x−3  có : Δ = 5²−4.m.(−3)=25+12m

Để mx²+5x−3 ≤ 0 ∀ x ϵ R thì :

Δ < 0  và m < 0 ⇒ m <