Slide bài giảng toán 10 chân trời bài 1: Số gần đúng và sai số
Slide điện tử bài 1: Số gần đúng và sai số. Kiến thức bài học được hình ảnh hóa, sinh động hóa. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 10 Chân trời sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 1: SỐ GẦN ĐÚNG VÀ SAI SỐ
1. SỐ GẦN ĐÚNG
Bài 1: Hãy đo chiều dài của bàn học bạn đang sử dụng.
Trả lời rút gọn:
Tự thực hiện
Bài 2: Trong trích đoạn một báo cáo tài chính dưới đây, theo bạn số nào là số đúng, số nào là số gần đúng?
Trong tháng 01/2021 có 47 dự án được cấp phép mới với số vốn đăng kí đạt gần 1,3 tỉ USD, giảm khoảng 81,8% về số dự án và 70,% về số vốn đăng kí so với cùng kì năm trước; 46 lượt dự án đã cấ phép từ các năm trước đăng kí điều chỉnh vốn đầu tư với số vốn tăng thêm trên 0,5 tỉ USD, tăng gần 41,4%.
Trả lời rút gọn:
Số đúng: 47 dự án, 46 lượt dự án
Số gần đúng: 1,3 tỉ USD; 81,8%; 70,3%; 0,5 tỉ USD và 41,4%.
2. SAI SỐ TUYỆT ĐỐI VÀ SAI SỐ TƯƠNG ĐỐI
Sai số tuyệt đối
Bài 1: Vinh và Hoa đo chiều dài trang bìa của một quyển sổ (Hình 2). Vinh đọc kết quả là 21cm. Hoa đọc kết quả là 20, cm. Kết quả của bạn nào có sai số nhỏ hơn?
Trả lời rút gọn:
Kết quả bạn Hoa sai số nhỏ hơn.
Bài 2:Cho biết 1,41 < 
< 1,42. Hãy tính độ dài đường chéo của một hình vuông có cạnh bằng 10 cm và xác định độ chính xác kết quả tìm được.
Trả lời rút gọn:
Độ dài đường chéo hình vuông = 
= 14,15 (cm)
Độ dài đúng, kí hiệu là 
, của hình vuông:
10. 1,41 < 
< 10. 1,42 hay 14,1 < 
< 14,2.
=> 14,1 - 14,15 < 
- l < 14,2 - 14,15,
|
- l| < 0,05.
Độ dài đường chéo hình vuông là 14,15 
0,05 (cm).
Bài 3: Một tấm bìa có dạng hình chữ nhật với kích thước được in như trong Hình 3.
a. Hãy cho biết kích thước chiều dài và chiều rộng của tấm bìa nằm trong khoảng nào.
b. Tính diện tích của tấm bìa.
Trả lời rút gọn:
a. Chiều dài khoảng từ 238 đến 142 mm; chiều rộng khoảng từ 168 đến 172 mm.
b. Diện tích của tấm bìa là: 170. 240 = 40 800 ± 4 (mm2)
Sai số tương đối
Bài 4: Vào năm 2015, các nhà khoa học trên thế giới ước lượng độ tuổi của vũ trụ là 13 799 ± 21 triệu năm.
Trọng tài bấm thời gian chạy 100m của một vận động viên là 10,3 ± 0,1 giây.
Theo bạn, trong hai phép đo trên, phép đo nào có độ chính xác cao hơn?
Trả lời rút gọn:
So sánh sai số tuyệt đối, phép đo trọng tài chính xác hơn các nhà khoa học.
So sánh hai tỉ số
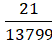= 0,0015... và 
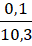= 0,0097..., phép đo của các nhà khoa học có tỉ số giữa độ chính xác và số gần đúng nhỏ hơn.
Bài 5: Hãy ước lượng sai số tương đối trong phép đo tuổi của vũ trụ và thời gian chạy của vận động viên ở Khám phá 3.
Trả lời rút gọn:
+ 
= 
0,15% + 
= 
0,97%.
3. SỐ QUY TRÒN
Quy tắc làm tròn số
Bài 1: Hãy quy tròn số 
= 5496 đến hàng chục và ước lượng sai số tương đối.
Trả lời rút gọn:
Quy tròn số 
= 5496 đến hàng chục: 5500.
Sai số tuyệt đối là  =  | Sai số tương đối là     0,09% |
Bài 2: Hãy viết số quy tròn của số gần đúng trong những trường hợp sau:
a. 318 081 ± 2 000; b. 18,0113 ± 0,003.
Trả lời rút gọn:
a. Hàng lớn nhất của độ chính xác d = 2 000 là hàng nghìn
=> Quy tròn số đến hàng chục nghìn.
Vậy số quy tròn của 318 081 là 320 000.
b. Hàng lớn nhất của độ chính xác d = 0,003 là hàng phần nghìn
=> Quy tròn số đến hàng phần trăm.
=> Vậy số quy tròn của số 18,0113 là 18,01.
Bài 3: Hãy xác định số gần đúng của các số sau với độ chính xác d = 0,0001.
a. 
= 
= 1,8181818...; b. 
= 1 - 
= -1,6457513...
Trả lời rút gọn:
a. Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,0001 là hàng phần chục nghìn. Quy tròn | b. Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,0001 là hàng phần chục nghìn. Quy tròn |
BÀI TẬP CUỐI SGK
Bài tập 1. Ở Babylon, một tấm đất sét có niên đại khoảng 1900 - 1600 trước Công nguyên đã ghi lại một phát biểu hình học, trong đó ám chỉ ước lượng số π bằng 
= 3,1250. Hãy ước lượng sai số tuyệt đối và sai số tương đối của giá trị gần đúng này, biết 3,141 < π < 3,142.
Trả lời rút gọn:
- Sai số tuyệt đối: | - Sai số tương đối là: |
Bài 2. Cho số gần đúng a = 6 547 với độ chính xác d = 100. Hãy viết số quy tròn của số a và ước lượng sai số tương đôi của số quy tròn đó.
Trả lời rút gọn:
Hàng lớn nhất của độ chính xác d = 100 là hàng trăm
=> Quy tròn số a đến hàng nghìn
Vậy tròn của a là 7 000.
Sai số tương đối của số quy tròn: 
= 
1,43%
Bài 3. Cho biết 
= 1,7320508...
a. Hãy quy tròn 
đến hàng phần trăm và ước lượng sai số tương đối.
b. Hãy tìm số gần đúng của 
với độ chính xác 0,003.
c. Hãy tìm số gần đúng của 
với độ chính xác đến hàng phần chục.
Trả lời rút gọn:
a) Quy tròn số 
= 
= 1,7320508... đến hàng phần trăm
-> số gần đúng là 1,73 (a < 
< 1,735)
=> Sai số tuyệt đối là: 
=
< 0,005.
Sai số tương đối là: 
0,3%
b) Hàng của chữ số khác 0 đầu tiên bên trái của d = 0,003 là hàng phần nghìn. Quy tròn 
đến hàng phần nghìn -> số gần đúng của 
= 1,732.
c) Quy tròn 
đến hàng phần chục nghìn -> gần đúng của 
= 1,7321.
Bài 4. Hãy viết số quy tròn của số gần đúng trong những trường hợp sau:
a. 4 536 002 ± 1 000;
b. 10,05043 ± 0,002.
Trả lời rút gọn:
a. Hàng lớn nhất của độ chính xác d = 1 000 là hàng nghìn -> Quy tròn số a đến hàng chục nghìn | Hàng lớn nhất của độ chính xác d = 0,002 là hàng phần nghìn -> Quy tròn số a đến hàng phần trăm. |
Vậy số quy tròn của a là 4 540 000. | Vậy số quy tròn của a là 10,05. |
Bài 5. Một tam giác có 3 cạnh đo được như sau: a = 5,4cm ± 0,2 cm; b = 7,2cm ± 0,2cm và c = 9,7cm ± 0,1cm. Tính chu vi của tam giác đó.
Trả lời rút gọn:
Chu vi của tam giác là: P = a + b + c = 5,4 + 7,2 + 9,7 = 22,3 (cm)
cận trên : (5,4 + 0,2) + (7,2 + 0,2) + (9,7 + 0,1) = 22,8 (cm)
cận dưới : (5,4 - 0,2) + (7,2 - 0,2) + (9,7 - 0,1) = 21,8 (cm)
hay 21,8 ≤ P ≤ 22,8
⇒ Sai số tuyệt đối của P là |P - P0| ≤ 0,5 cm
Vậy chu vi của tam giác là 22,3 ± 0,5 (cm).
Bài 6. Chiếc kim màu đỏ chỉ cần nặng của bác Phúc (Hình 5). Hãy viết cân nặng của bác Phúc dưới dạng số gần đúng với độ chính xác 0,5kg.
Trả lời rút gọn: 64kg ± 0,5kg
Slide bài giảng lớp 10 cánh diều
Slide bài giảng lớp 10 chân trời sáng tạo
Slide bài giảng lớp 10 kết nối tri thức
