Slide bài giảng toán 10 chân trời bài: Bài tập cuối chương IX

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG 9

Bài 1: Trong mặt phẳng Oxy, cho bốn điểm A(2; 1), B(1; 4), C(4; 5), D(5; 2).

a. Chứng minh ABCD là hình vuông. 

b. Tìm tọa độ tâm I của hình vuông ABCD.

Trả lời rút gọn: 

a) Ta có: = (-1; 3), = (-1; 3) =  

ABCD là hình bình hành.

Lại có: = (3; 1) . = -1. 3 + 3. 1 = 0

hay AB AD

Hình bình hành ABCD là hình chữ nhật.

Ta có: AD = || = =

          AB = || = =

AB = AD Hình chữ nhật ABCD là hình vuông (đpcm).

b) Tâm I của hình vuông ABCD là trung điểm của AC I = (; ) I = (3; 3)

Vậy I = (3; 3).

Bài 2: Cho AB và CD là dây cung vuông góc tại E của đường tròn (O). Vẽ hình chữ nhật AECF. Dùng phương pháp tọa độ để chứng minh EF vuông góc với DB.

Trả lời rút gọn: 

Chọn hệ tọa độ Oxy như hình vẽ. A(a; 0), B(b; 0), C(0; c), D(0; d). Hai dây cung AB và CD vuông góc với nhau tại E (trùng với gốc tọa độ O).

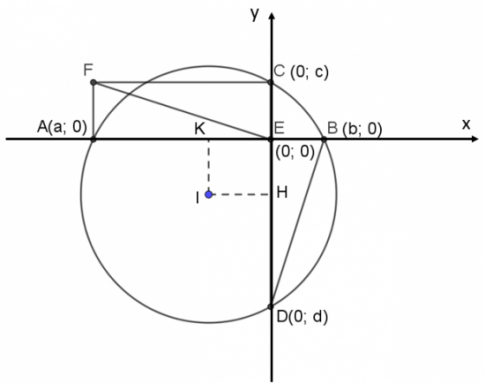
Vì ACEF là hình chữ nhật nên F(a; c). 

Gọi I là tâm đường tròn (O), K và H lần lượt là chân đường cao hạ từ I tới AB, CD.

K là trung điểm của AB K = (; 0)

     H là trung điểm của CD H = (0; )

I = (; )

Ta có: = (a - ; -) = (; -)

          = ( -; c - ) = (-;

Vì IA = IC (=R) + = +

+ = +

     Độ dài trục thực là: 2a = 2. 4 = 8; độ dài trục ảo là: 2b = 2. 3 = 6.

Bài 12: Viết phương trình chính tắc của hypebol thoả mãn từng điều kiện sau:

a. Đỉnh (3; 0), tiêu điểm (5; 0);

b. Độ dài trục thực 8, độ dài trục ảo 6.

Trả lời rút gọn: 

a. Đỉnh (3; 0) ⇒ a = 3; tiêu điểm (5; 0) ⇒  c = 5.

⇒ b = = 4

⇒ Phương trình hypebol là: =1.

b. Ta có: 2a = 8; 2b = 6 ⇒ a = 4; b = 3

⇒ Phương trình hypebol là: =1.

Bài 13: Tìm tọa độ tiêu điểm, phương trình đường chuẩn của các parabol sau:

a. y²=12x;                       b. y²=x.

Trả lời rút gọn: 

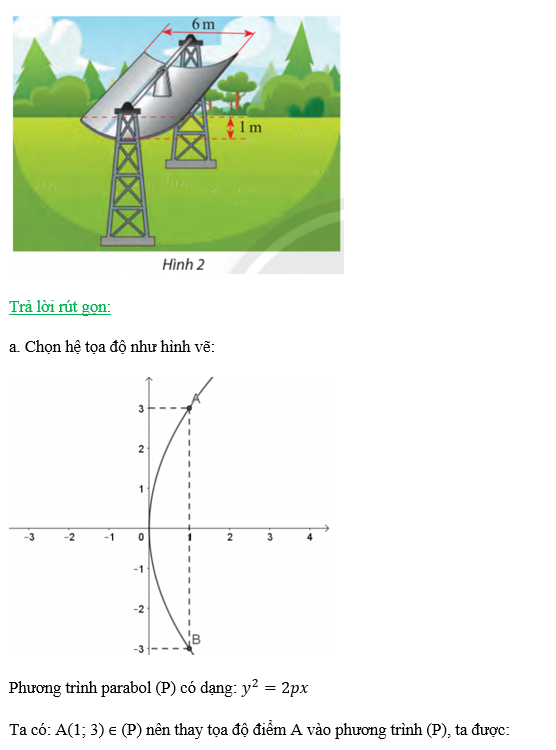
a. Phương trình parabol có dạng: y²=2px ⇒ p = 6

⇒ Tọa độ tiêu điểm là (3; 0) và phương trình đường chuẩn là x+3=0.

b. Phương trình parabol có dạng: y²=2px ⇒ p =

⇒ Tọa độ tiêu điểm là ( ; 0) và phương trình đường chuẩn là x+=0.

Bài 14: Viết phương trình chính tắc của parabol thảo mãn từng điều kiện sau:

a. Tiêu điểm (4; 0);

b. Đường chuẩn có phương trình x=−;

c. Đi qua điểm (1; 4);

d. Khoảng cách từ tiêu điểm đến đường chuẩn bằng 8.

Trả lời rút gọn: 

a. Tiêu điểm (4; 0) ⇒ p = 8

⇒ Phương trình parabol (P) là: y²=16x.

b. Đường chuẩn có phương trình x=− ⇒ p =

⇒ Phương trình parabol (P) là: y² = x.

c. Phương trình parabol (P) có dạng: y²=2px.

Vì (P) đi qua điểm (1; 4) nên thay tọa độ (1; 4) vào phương trình của (P), ta được:

4² = 2p. 1 ⇒ p = 8.

⇒ Phương trình parabol (P) là: y²=16x.

d. Ta có: F(; 0), phương trình đường chuẩn Δ: x +=0

d(F, Δ) = 8 ⇔ = 8 ⇔ p = 8

⇒ Phương trình parabol (P) là: y²=16x.

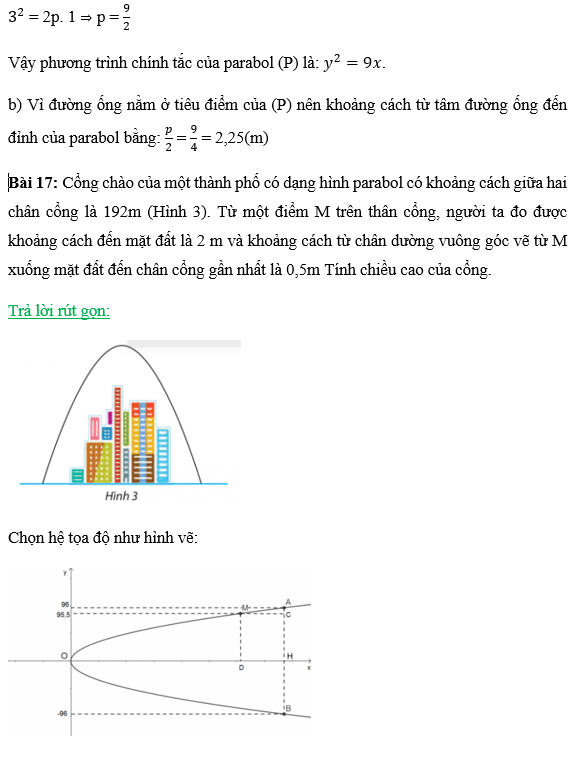
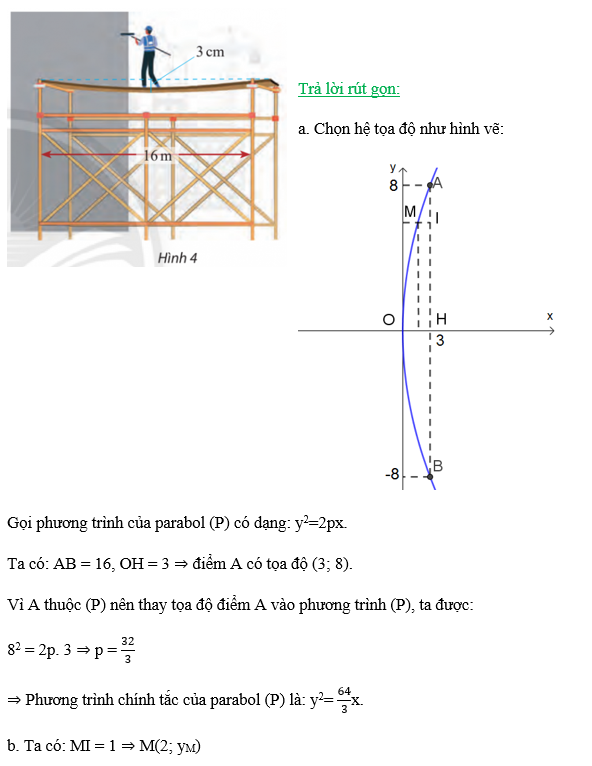
Vì M ∈ (P) nên thay tọa độ điểm M vào phương trình (P), ta được: 

= . 2 ⇒ y_M = 

⇒ M(2; ) ⇒ OM =≈ 6,83.

Vậy điểm M có độ võng 1 cm cách tấm ván gỗ khoảng 6,83m.