Bài tập về tính tiện tích xung quanh, diện tích toàn phần của hình chóp đều

1.

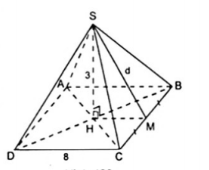
Xét hình chóp tứ giác đều S.ABCD đáy là hình vuông ABCD có cạnh BC = 8cm đường cao SH = 3cm, chân đường cao H của hình chóp là tâm đường tròn đi qua các đỉnh của hình vuông ABCD nên H là trung điểm của AC. Áp dụng công thức:

S_xq = p.d với p = 2.8 = 16 (cm)

Gọi M là trung điểm của BC thì SM là đường cao của mặt bên (SBC) nên SM = d là trung đoạn của hình chóp, đồng thời HM là đường trung bình của $\Delta $BCD. Do đó HM = $\frac{1}{2}$DC = 4 (cm)

Vì SH là đường cao của hình chóp đều nên SH $\perp $ HM, hay $\Delta $SHM vuông ở H.

Theo định lí Py-ta-go $\Delta $AHM vuông ở H có:

$SM^{2}=HM^{2}+SH^{2}$ hay $d^{2}=3^{2}+4^{2}\Leftrightarrow d=5$ (cm)

Vậy S_xq = 16.5 = 80 (cm$^{2}$)

2.

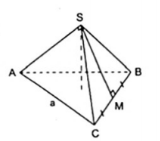
Xét hình chóp S.ABC có AB = BC = CA = a, các mặt bên là các tam giác vuông cân tại S.

Gọi M là trung điểm của BC thì SM vừa là đường trung tuyến, vừa là đường cao vẽ từ đỉnh của mặt bên (SBC), nên SM = d là trung đoạn của hình chóp.

Áp dụng định lí về trung tuyến ứng với cạnh huyền vào $\Delta $SBC vuông ta được:

d = SM = $\frac{1}{2}BC=\frac{a}{2}$

Vậy S_xq = p.d = $\frac{3}{2}a.\frac{a}{2}=\frac{3}{4}a^{2}$