Bài tập về tính thể tích, tính một yếu tố của hình chóp tam giác, lúc giác đều

6.

Xét hình chóp tam giác đều S.ABC có tất cả các cạnh bằng a.

Áp dụng công thức tính thể tích hình chóp:

V = $\frac{1}{3}$S.h

Theo giả thiết cạnh đáy của tam giác đều là BC = a nên ta có AI = $\frac{a\sqrt{3}}{2}$ và SABC = $\frac{a^{2}\sqrt{3}}{4}$

Kẻ đường cao SH của chóp đều. Ta có BH = AH = $\frac{a\sqrt{3}}{3}$

Áp dụng định lí Py-ta-go vào $\Delta $SHB vuông ở H, ta được:

$SB^{2}=HB^{2}+SH^{2}$ hay $a^{2}=SH^{2}+\left ( \frac{a\sqrt{3}}{3} \right )^{2}$

$\Leftrightarrow SH=\frac{a\sqrt{6}}{3}$

Vậy V = $\frac{1}{3}.\frac{a^{2}\sqrt{3}}{4}.\frac{a\sqrt{6}}{3}=\frac{a^{3}\sqrt{2}}{12}$

7. 

Áp dụng công thức tính thể tích hình chóp:

V = $\frac{1}{3}$S.h

Theo giả thiết cạnh đáy của tam giác đều là BC = 4cm nên ta có:

AI = $\frac{4\sqrt{3}}{2}=2\sqrt{3}$ (cm); S_ABC = $ \frac{4^{2}\sqrt{3}}{4}=4\sqrt{3} (cm^{2})$

Kẻ đường cao SH của chóp đều áp, ta được:

BH = AH = $\frac{2}{3}.2\sqrt{3}=\frac{4\sqrt{3}}{3}$ (cm)

Áp dụng định lí Py-ta-go vào $\Delta $SHB vuông ở H, ta được:

$SB^{2}=HB^{2}+SH^{2}$ hay $(\sqrt{13})^{2}=SH^{2}+\left ( \frac{4\sqrt{3}}{3} \right )^{2}$

$\Leftrightarrow SH=\frac{\sqrt{69}}{3}$ (cm)

Vậy V = $\frac{1}{3}.4\sqrt{3}.\frac{\sqrt{69}}{3}=\frac{4\sqrt{23}}{3} (cm^{3})$

8.

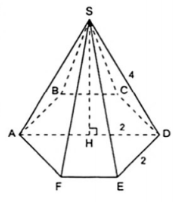
Áp dụng công thức tính thể tích hình chóp :

V = $\frac{1}{3}$S.h

Lục giác đều cạnh 2cm có diện tích bằng 6 lần diện tích tam giác đều cạnh 2cm, do đó 

S = $6.\frac{2^{2}.\sqrt{3}}{4}=6\sqrt{3}(cm^{2})$

Áp dụng định lí Py-ta-go vào $\Delta $SHD vuông ở H, ta được:

$SD^{2}=HD^{2}+SH^{2}$ hay $4^{2}=2^{2}+SH^{2}$

$\Leftrightarrow SH=2\sqrt{3}$ (cm)

Vậy V = $\frac{1}{3}.6\sqrt{3}.2\sqrt{3}=12(cm^{3})$