Bài tập về tính diện tích hình thang
1. Tính diện tích hình thang vuông ABCD ($\widehat{A}=\widehat{D}=90^{\circ}$), biết $\widehat{C}=45^{\circ}$, AB = 2cm và CD = 4cm.
2. Tính diện tích hình thang ABCD biết AB = 3cm, BC = 8cm, CD = 12cm và $\widehat{C}=30^{\circ}$
3. Cho hình thang cân ABCD (AB // CD, AB < CD) biết chiều cao AH = 8cm và HC = 12cm.
4. Chứng minh rằng diện tích tam giác có cạnh đáy là cạnh bên của hình thang là trung điểm của cạnh bên kia thì bằng một nửa diện tích của hình thang đó.
1.
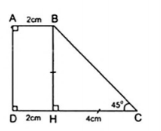
Kẻ đường cao BH thì tứ giác ABHD có ba góc vuông nên nó là hình chữ nhật.
$\Rightarrow $ DH = AB = 2cm. Do đó HC = 6 -2 = 4.
$\Delta $BCH có $\widehat{C}=45^{\circ}$ nên vuông cân ở H
$\Rightarrow $ BH = HC
Áp dụng công thức tính diện tích hình thang ta được:
S = $\frac{(AB+CD).BH}{2}=\frac{(2+6).4}{2}=16(cm^{2})$
2.

Kẻ đường cao BH thì tứ giác ABHD có ba góc vuông nên nó là hình chữ nhật, suy ra DH = AB = 3cm.
Do đó HC = 12 - 3 = 9 (cm)
Vì $\Delta $BCH vuông tại H có $\widehat{C}=30^{\circ}$ nên BH = $\frac{1}{2}$BC = 4 (cm)
Vậy diện tích hình thang ABCD là:
S = $\frac{(AB + CD).BH}{2}=\frac{(3+12).4}{2}=30(cm^{2})$
3.
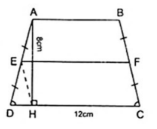
Gọi E, F lần lượt là trung điểm của AD và BC thì EF là đường trung bình của hình thang ABCD nên EF // CD và 2EF = AB + CD.
Xét $\Delta $ADH vuông tại H có E là trung điểm của cạnh huyền AD nên EH = DE = $\frac{1}{2}$AD.
Mà AD = BC; FC = $\frac{1}{2}$BC
$\Rightarrow $ EH = FC (1)
$\Delta $EDH có ED = EH nên $\Delta $EDH cân tại E $\Rightarrow \widehat{EDH}=\widehat{EHD}$
Mà $\widehat{EDH}=\widehat{FCE}$ (hình thang ABCD cân)
$\Rightarrow \widehat{FCH}=\widehat{EHD}$
$\Rightarrow $ EH // FC (2)
Từ (1) và (2) ta được EHCF là hình bình hành.
$\Rightarrow $ EF = HC = 8 (cm)
Vậy ta được diện tích hình thang ABCD là:
S = $\frac{(AB+CD).AH}{2}=\frac{2.EF.AH}{2}=EF.AH = 8.12 = 96(cm^{2})$
4.
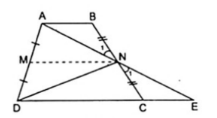
Xét hình thang ABCD (AB // CD) có M, N lần lượt là trung điểm của AD và BC.
Ta phải chứng minh $S_{AND}= \frac{1}{2}S_{ABCD}$
Ta có: $\Delta $ABN = $\Delta $ECN (g.c.g)
$\Rightarrow S_{ABN}=S_{ECN}$ (1) và AN = NE.
$\Rightarrow S_{ABN}+S_{ANCD}=S_{ECN}+S_{ANCD}$
$\Rightarrow S_{ABCD}=S_{AED}$ (2)
Mà $S_{AND}=S_{NED}$ (3) vì chung chiều cao kẻ từ D đến AE, đáy bằng nhau.
Từ (2) và (3) suy ra $S_{AND}=\frac{1}{2}S_{AED}=\frac{1}{2}S_{ABCD}$

Bình luận