Bài tập về sử dụng các trường hợp đồng dạng của tam giác vuông để tính toán

4.

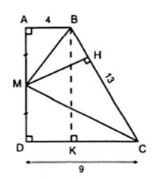
Kẻ BK $\perp $ CD (K thuộc CD) thì tứ giác ABKD là hình có 3 góc vuông nên nó là hình chữ nhật.

Do đó DK = AB = 4cm

$\Rightarrow $ KC = DC - DK = 9 - 4 = 5 (cm)

$\Delta $KBC vuông tại K theo định lí Py-ta-go ta có:

$BC^{2}=CK^{2}+KB^{2}$ hay $13^{2}=5^{2}+KB^{2}$

$\Rightarrow $ KB = 12 (cm), nên AD = BK = 12 (cm)

M là trung điểm của AD nên AM = MD = $\frac{1}{2}$AD = 6(cm)

Xét $\Delta $AMB và $\Delta $DCM có:

$\frac{AB}{AM}=\frac{4}{6}=\frac{6}{9}=\frac{MD}{DC}$

$\Rightarrow \Delta AMB \sim  \Delta DCM$

$\Rightarrow \widehat{AMB}=\widehat{DCM}$

Mà $\widehat{DMC}+\widehat{DCM}=90^{\circ}$

$\Rightarrow \widehat{AMB}+\widehat{DCM}=90^{\circ}$

$\Rightarrow \widehat{BMC}=90^{\circ}$

Kẻ MH $\perp $ BC thì MH là khoảng cách từ M đến BC.

Áp dụng định lí Py-ta-go vào $\Delta $ABM và $\Delta $DMC vuông ta được:

$BM^{2}=MA^{2}+AB^{2}=6^{2}+4^{2}=52$

$BM^{2}=CD^{2}+DM^{2}=9^{2}+6^{2}=117$

$\Rightarrow BM=2\sqrt{13}$ (cm) và $CM=3\sqrt{13}$ (cm)

Do đó ta có:

  BM.MC = MH.BC

$\Rightarrow MH=\frac{BM.MC}{BC}=\frac{2\sqrt{13}.3\sqrt{13}}{13}=6$ (cm)

5. 

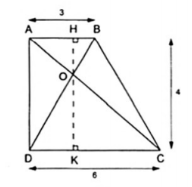
Kẻ OH $\perp $ AB kéo dài cắt CD ở K thì OK $\perp $ CD.

Nên OH, OK thứ tự là các đường cao của $\Delta $OAB và $\Delta $OCD

Từ giả thiết AB // CD ta có $\Delta OAB\sim \Delta OCD$ nên $k=\frac{AB}{CD}=\frac{3}{6}=\frac{1}{2}$

Áp dụng kết quả tỉ số đường cao tương ứng bằng tỉ số đồng dạng ta được:

$\frac{OH}{OK}=\frac{1}{2}\Rightarrow OH = \frac{1}{3}HK$ và $OK=\frac{2}{3}HK$.

Mà HK = 4(cm) $\Rightarrow OH = \frac{4}{3}(cm)$ và $OK=\frac{8}{3}(cm)$

Vậy $S_{OAB}=\frac{1}{2}AB.OH=\frac{1}{2}.3.\frac{4}{3}=2(cm^{2})$

    $S_{OCD}=\frac{1}{2}CD.OK=\frac{1}{2}.6.\frac{8}{3}=8(cm^{2})$

6.

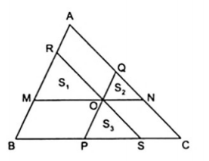
Từ giả thiết MO // BC, RO // AC, QO // AB, ON // BC, OP // AB, OS // AC nên $\Delta $RMO, $\Delta $QON; $\Delta $OPS cung đồng dạng với $\Delta $ABC và các tứ giác AQOR, ONCS và MOPB là các hình bình hành.

Áp dụng tính chất về cạnh vàoo các hình bình hành trên ta được:

MO = BP; ON = SC

Áp dụng định lí về tỉ số diện tích hai tam giác đồng dạng ta được:

$\frac{S_{1}}{S}=\left ( \frac{MO}{BC} \right )^{2}=\left ( \frac{BP}{BC} \right )^{2}\Rightarrow \frac{\sqrt{S_{1}}}{\sqrt{S}}=\frac{BP}{BC}$ (1)

Tương tự: $\frac{\sqrt{S_{2}}}{\sqrt{S}}=\frac{SC}{BC}$ (2)

          $\frac{\sqrt{S_{3}}}{\sqrt{S}}=\frac{PS}{BC}$ (3)

Từ (1), (2) và (3) ta được: $\frac{\sqrt{S_{1}}}{\sqrt{S}}+\frac{\sqrt{S_{1}}}{\sqrt{S}}+\frac{\sqrt{S_{1}}}{\sqrt{S}}=\frac{BP}{BC}+\frac{SC}{BC}+\frac{PS}{BC}=\frac{BC}{BC}=1$

$\Rightarrow \sqrt{S_{1}}+\sqrt{S_{2}}+\sqrt{S_{3}}=\sqrt{S}$

7.

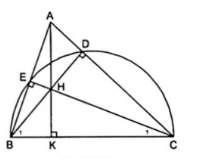
a) $\Delta $BKH và $\Delta $BDC có:

chung $\widehat{DBC}$

$\widehat{K}=\widehat{D}=90^{\circ}$

$\Rightarrow \Delta BKH \sim \Delta BDC$ (g-g)

$\Rightarrow \frac{BK}{BD}=\frac{BH}{BC}\Rightarrow BD.BH=BC.BK$ (1)

b) $\Delta $CKH và $\Delta $CEB có:

chung $\widehat{DBC}$

$\widehat{K}=\widehat{E}=90^{\circ}$

$\Rightarrow \Delta CKH \sim \Delta CEB$ (g-g)

$\Rightarrow \frac{CK}{CE}=\frac{CH}{BC}\Rightarrow CE.CH=CB.CK$ (2)

c) Cộng theo vế các đẳng thức (1) và (2) ta được:

BD.BH + CE.CH = BC.BK + CB.CK = BC.(BK+CK) = BC.BC = BC$^{2}$