Video giảng Toán 10 chân trời bài tập cuối chương III

Tóm lược nội dung

BÀI TẬP CUỐI CHƯƠNG III

Chào mừng các em đến với bài học ngày hôm nay!

Thông qua video này, các em sẽ nắm được các kiến thức và kĩ năng như sau:

- Hàm số. Tập xác định và tập giá trị của hàm số

- Đồ thị hàm số. Hàm số đồng biến, hàm số nghịch biến.

- Hàm số bậc hai. Đồ thị hàm số bậc hai. 

- Sự biến thiên của hàm số bậc hai. 

- Ứng dụng của hàm số bậc hai

HOẠT ĐỘNG KHỞI ĐỘNG:

Trước khi vào bài học, cô yêu cầu cả lớp chia nhóm để thực hiện yêu cầu: 

+ Cho ví dụ về hàm số bậc hai. 

+ Xác định tập xác định và tập giá trị của hàm số. 

+ Hàm số đó đồng biến trên khoảng nào, nghịch biến trên khoảng nào?

+ Xác định tính chất biến thiên của hàm số bậc hai. 

HOẠT ĐỘNG KHÁM PHÁ

Nội dung 1: Luyện tập

Cô muốn cả lớp thực hiện yêu cầu sau: suy nghĩ trả lời nhanh Bài 1 (SGK – tr59).

- GV tổ chức cho HS hoạt động làm bài 2, 3, 5 (SGK – tr59). 

Video trình bày nội dung:

Bài 1.

a) Tập xác định của hàm số D =

b) Biểu thức có nghĩa khi và chỉ khi + 1 0 -1 (luôn đúng x )

Vậy tập xác định của hàm số là D =

c) Biểu thức có nghĩa khi và chỉ khi x 0

Vậy tập xác định của hàm số là D = \ {0}

Bài 2. 

a) y = (1 - 3m) + 3

Để hàm số trên là hàm số bậc hai 1 - 3m 0 m  

Vậy m  

b) y = (4m - 1) = (4m - 1)( - 14x + 49) = (4m - 1) - (56m - 14)x + 49(m - 1)

Để hàm số trên là hàm số bậc hai 4m - 1 0 m  

c) y = 2( + 1) + 11 - m = 2 + 13 - m

Để hàm số trên là hàm số bậc hai 2 0 (luôn đúng)

Vậy hàm số trên là hàm số bậc hai m .

Bài 3. 

a) y = - 4x + 3

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = - 4x + 3 là một parabol (P):

• Có đỉnh S(2; -1) 

• Có trục đối xứng là đường thẳng x = 2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

• Bề lõm quay lên trên vì a = 1 > 0;

• Cắt trục tung tại điểm có tung độ bằng 3, tức là đồ thị đi qua điểm có tọa độ (0; 3).

• Phương trình 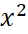- 4x + 3 = 0 có hai nghiệm phân biệt à 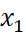= 1 và 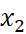= 3 nên đồ thị hàm số cắt trục hoành tại hai điểm có tọa độ (1; 0) và (3; 0)

Ta được đồ thị như sau:

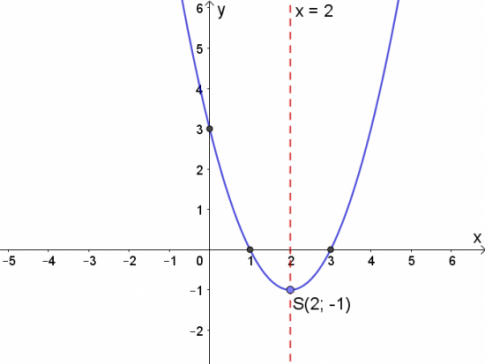
b) y = -  - 4x + 5

Trong mặt phẳng tọa độ Oxy, đồ thị hàm số bậc hai y = f(x) = -  - 4x + 5 là một parabol (P):

• Có đỉnh S(-2; 9) 

• Có trục đối xứng là đường thẳng x = -2 (đường thẳng này đi qua đỉnh S và song song với trục Oy);

• Bề lõm quay xuống dưới vì a = -1 < 0;

• Cắt trục tung tại điểm có tung độ bằng 5, tức là đồ thị đi qua điểm có tọa độ (0; 5).

………..

Nội dung video Bài tập cuối chương III còn nhiều phần rất hấp dẫn và thú vị. Hãy cùng đăng kí để tham gia học bài và củng cố kiến thức thông qua hoạt động luyện tập và vận dụng trong video.