Slide bài giảng Toán 11 kết nối Bài 6: Cấp số cộng

Tóm lược nội dung

BÀI 6. CẤP SỐ CỘNG

1. ĐỊNH NGHĨA

Bài 1: Nhận biết cấp số cộng

Cho dãy số () gồm tất cả các số tự nhiên lẻ, xếp theo thứ tự tăng dần.

1. Viết năm số hạng đầu của dãy số.
2. Dự đoán công thức biểu diễn số hạng 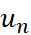theo số hạng .

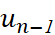Giải rút gọn: 

a) Năm số hạng đầu của dãy số là năm số tự nhiên lẻ đầu tiên và đó là: .

b) Nhận thấy trong dãy số (u_n), số hạng sau hơn số hạng liền trước 2 đơn vị.

Công thức biểu diễn số hạng theo số hạng u_{n – 1} là là

Bài 2: Dãy số không đổi a, a, a, … có phải là một cấp số cộng không?

Giải rút gọn: 

Dãy số không đổi là một cấp số cộng với công sai .

=> Đây là một dãy số hằng.

Bài 3: Cho dãy số () với = -2n +3. Chứng minh rằng () là một cấp số cộng.  Xác định số hạng đầu và công sai của cấp số cộng này.

Giải rút gọn: 

Do đó, với mọi

Vậy ;

2. SỐ HẠNG TỔNG QUÁT

Bài 1: Công thức số hạng tổng quát của cấp số cộng

Cho cấp số cộng () với số hạng đầu và công sai d.

1. Tính các số hạng 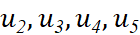theo và d.
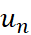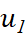2. Dự đoán công thức tính số hạng tổng quát theo và d.

Giải rút gọn: 

a) 

• 
•  
•  
• .

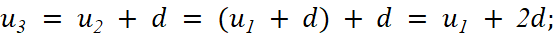
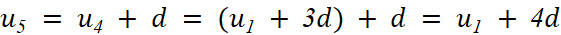b) Công thức số hạng tổng quát theo và là:

Bài 2: Cho dãy số () với = 4n -3. Chứng minh rằng () là một cấp số cộng. Xác định số hạng đầu và công sai d của cấp số cộng này. Từ đó viết số hạng tổng quát dưới dạng = .

Giải rút gọn: 

, ∀ .

Dãy số là một cấp số cộng với số hạng đầu ; Số hạng tổng quát là:

3. TỔNG N SỐ HẠNG ĐẦU CỦA MỘT CẤP SỐ CỘNG

Bài 1: Xây dựng công thức tính tổng n số hạng đầu của cấp số cộng

Cho cấp số cộng () với số hạng đầu và công sai d.

Để tính tổng của n số hạng đầu 

Giải rút gọn: 

a)

b)

c) 

Bài 2: Anh Nam được nhận vào làm việc ở một công ty về công nghệ với mức lương khởi điểm là 100 triệu đồng một năm. Công ty sẽ tăng thêm lương cho anh Nam mỗi năm là 20 triệu đồng. Tính tổng số tiền lương mà anh Nam nhận được sau 10 năm làm việc cho công ty đó.

Giải rút gọn: 

Số tiền lương anh Nam nhận được mỗi năm lập thành một cấp số cộng, gồm 10 số hạng, với số hạng đầu u₁ = 100 và công sai d = 20.

Tổng 10 số hạng đầu của cấp số cộng này là

Vậy số tiền lương mà anh Nam nhận được sau 10 năm làm việc ở công ty này là 1 900 triệu đồng hay 1 tỷ 900 triệu đồng.

CÒN TIẾP…