Slide bài giảng Toán 11 kết nối Bài 5: Dãy số
Slide điện tử Bài 5: Dãy số. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 5. DÃY SỐ
1. ĐỊNH NGHĨA DÃY SỐ
Bài 1: Nhận biết dãy số vô hạn
Viết năm số chính phương đầu theo thứ tự tăng dần. Từ đó, dự đoán công thức tính số chính phương thứ n.
Từ công thức nhận được, ta có quy tắc để viết được dãy gồm tất cả các số chính phương
Đáp án:
Năm số chính phương đầu theo thứ tự tăng dần: ![]() .
.
Số chính phương
Tiếp tục như trên, ta dự đoán được công thức tính số chính phương thứ n là ![]() với
với ![]()
Bài 2: Nhận biết dãy số hữu hạn
- Liệt kê tất cả các số chính phương nhỏ hơn 50 và sắp xếp chúng theo thứ tự từ bé đến lớn.
- Viết công thức số hạng
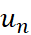 của các số tìm được ở câu a và nêu rõ điều kiện của n
của các số tìm được ở câu a và nêu rõ điều kiện của n
Đáp án:
a) Các số chính phương < 50 được sắp xếp theo thứ tự từ bé đến lớn là
![]() .
.
b) ![]() với
với ![]() và n ≤ 8.
và n ≤ 8.
Bài 3: a) Xét dãy số gồm tất cả các số tự nhiên chia cho 5 dư 1 theo thứ tự tăng dần. Xác định số hạng tổng quát của dãy số.
b) Viết dãy số hữu hạn gồm năm số hạng đầu của dãy số trong câu a. Xác định số hạng đầu và số hạng cuối của dãy số hữu hạn này.
Đáp án:
a) Xét số tự nhiên a ≠ 0, có a : cho 5 dư 1 => E số tự nhiên q khác 0 để ![]() .
.
Xét dãy số gồm tất cả các số tự nhiên ∶ cho 5 dư 1 theo thứ tự tăng dần.
=> ![]()
b) Dãy gồm năm số hạng đầu của dãy số trong câu a là: ![]()
số hạng đầu ![]() , số hạng cuối:
, số hạng cuối: ![]() .
.
2. CÁC CÁCH CHO MỘT DÃY SỐ
Bài 1: Nhận biết các cách cho một dãy số
Xét dãy số (![]() ) gồm tất cả các số nguyên dương chia hết cho 5, sắp xếp từ bé đến lớn: 5, 10, 15, 20, 25, 30,...
) gồm tất cả các số nguyên dương chia hết cho 5, sắp xếp từ bé đến lớn: 5, 10, 15, 20, 25, 30,...
- Viết công thưc số hạng tổng quát
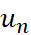 của dãy số
của dãy số - Xác định số hạng đầu và viết công thức tính số hạng thứ n theo số hạng thứ n - 1 của dãy số. Công thức thu được gọi là hệ thức truy hồi.
Đáp án:
a) ![]()
b) ![]() .
.
Công thức tính số hạng thứ n theo số hạng thứ ![]()
Bài 2:
a) Viết năm số hạng đầu của dãy số (![]() ) với số hạng tổng quát
) với số hạng tổng quát ![]() = n!.
= n!.
b) Viết năm số hạng đầu của dãy số Fibonacci (![]() ) cho bởi hệ thức truy hồi
) cho bởi hệ thức truy hồi
Đáp án:
a) Năm số hạng đầu của dãy số ![]() với số hạng tổng quát
với số hạng tổng quát ![]() là
là
![]()
![]()
![]()
![]()
![]()
b) Năm số hạng đầu của dãy số Fibonacci ![]() là
là
![]()
![]()
![]()
![]()
![]()
Chú ý
![]()
Để có hình ảnh trực quan về dãy số, ta thường biểu diễn các số hạng của nó trên trục số. Chẳng hạn, xét dãy số ![]() với
với ![]() . Năm số hạng đầu tiên của dãy số này là:
. Năm số hạng đầu tiên của dãy số này là:
![]() và được biểu diễn trên trục số như trên.
và được biểu diễn trên trục số như trên.
3. DÃY SỐ TĂNG, DÃY SỐ GIẢM VÀ DÃY SỐ BỊ CHẶN
Bài 1: Nhận biết dãy số tăng, dãy số giảm
- Xét dãy số (
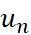 ) với
) với  = 3n -1. Tính
= 3n -1. Tính  và so sánh với
và so sánh với 
- Xét dãy số (
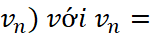
 . Tính
. Tính  và so sánh với
và so sánh với 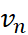
Đáp án:
a)
![]()
Hiệu ![]() có:
có: ![]() ,
,
=> ![]() .
.
Vậy ![]()
b) ![]() .
.
Hiệu ![]() ta có:
ta có:
![]()
![]()
![]() ℕ*
ℕ*
=> ![]()
Vậy ![]() .
.
Bài 2: Xét tính tăng, giảm của dãy số (![]() ), với
), với ![]() =
= ![]()
Đáp án:
![]()
![]()
![]()
=> ![]()
Vậy ![]() là dãy số giảm.
là dãy số giảm.
Bài 3: Nhận biết dãy số bị chặn
Cho dãy số (![]() ) với
) với ![]() ,
, ![]()
- So sánh
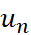 và 1.
và 1. - So sánh
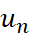 và 2.
và 2.
Đáp án:
a) ![]()
b) ![]()
=> ![]()
Do đó, ![]() .
.
Bài 4: Xét tính bị chặn của dãy số ![]() = 2n -1.
= 2n -1.
Đáp án:
un = 2n – 1 ≥ 1, ∀ n ∈ ℕ*.
Dãy số (un) bị chặn dưới.
Dãy số (un) không bị chặn trên vì không có số M nào thỏa mãn:
![]() = 2n – 1 ≤ M
= 2n – 1 ≤ M ![]()
Vậy dãy số ![]() bị chặn dưới và không bị chặn trên nên không bị chặn.
bị chặn dưới và không bị chặn trên nên không bị chặn.
Bài 5: Anh Thanh vừa được tuyển vào một công ty công nghệ, được cam kết lương năm đầu sẽ là 200 triệu đồng và lương mỗi năm tiếp theo sẽ được tăng thêm 25 triệu đồng. Gọi ![]() (triệu đồng) là lương và năm thứ n mà anh Thanh làm việc cho công ty đó. Khi đó ta có:
(triệu đồng) là lương và năm thứ n mà anh Thanh làm việc cho công ty đó. Khi đó ta có:
![]() = 200,
= 200, ![]() =
= ![]() + 25 với n ≥ 2
+ 25 với n ≥ 2
Đáp án:
a)
Vậy lương của anh Thanh vào năm thứ 5 làm việc cho công ty là 300 triệu đồng.
b) Ta có: ![]() ∀
∀ ![]()
=> ![]()
Vậy ![]() là dãy số tăng. Điều này có nghĩa là mức lương hàng năm của anh Thanh tăng dần theo thời gian làm việc
là dãy số tăng. Điều này có nghĩa là mức lương hàng năm của anh Thanh tăng dần theo thời gian làm việc
BÀI TẬP CUỐI SGK
Bài tập 2.1: Viết năm số hạng đầu và số hạng thứ 100 của các dãy số (![]() ) có số hạng tổng quát cho bởi:
) có số hạng tổng quát cho bởi:
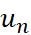 = 3n -2
= 3n -2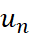 = 3.
= 3.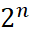
 =
= 
Đáp án:
a)
![]()
![]()
![]()
![]()
![]()
![]()
b)
![]()
![]()
![]()
![]()
![]()
![]() .
.
c)
![]()
![]()
![]()
![]()
![]()
![]()
Bài tập 2.2: Dãy số (![]() ) cho bởi hệ thức truy hồi...
) cho bởi hệ thức truy hồi...
Đáp án:
a) Năm số hạng đầu của dãy số là
![]()
![]()
![]()
![]()
![]() .
.
b)
![]() ;
;
![]()
![]()
![]()
![]()
=> công thức số hạng tổng quát của ![]() là
là ![]()
