Slide bài giảng Toán 11 kết nối Bài 3: Hàm số lượng giác
Slide điện tử Bài 3: Hàm số lượng giác. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 3. HÀM SỐ LƯỢNG GIÁC
1. ĐỊNH NGHĨA HÀM SỐ LƯỢNG GIÁC
Bài 1: Hoàn thành bảng sau:

Giải rút gọn:
x |
|
|
|
|
|
|
|
|
|
0 | 0 | 1 | 0 | KXĐ |
|
| 0 | KXĐ | 0 |
Bài 2: Tìm tập xác định của hàm số y = ![]() .
.
Giải rút gọn:
Biểu thức ![]() có nghĩa khi
có nghĩa khi ![]() tức là:
tức là:
![]()
Vậy tập xác định của hàm số ![]() là
là ![]() .
.
2. HÀM SỐ CHẴN, HÀM SỐ LẺ, HÀM SỐ TUẦN HOÀN
Bài 1: Cho hai hàm số ![]() và
và ![]() , với các đồ thị như hình dưới đây.
, với các đồ thị như hình dưới đây.
- Tìm các tập xác định
 ,
,  của các hàm số
của các hàm số  và
và 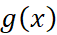 .
. - Chứng tỏ rằng
 =
= 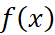 ,
,  . Có nhận xét gì về tính đối xứng của đồ thị hàm số y =
. Có nhận xét gì về tính đối xứng của đồ thị hàm số y =  đối với hệ trục toạ độ Oxy?
đối với hệ trục toạ độ Oxy? - Chứng tỏ rằng g(-x) = - g(x),
 . Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục toạ độ Oxy?
. Có nhận xét gì về tính đối xứng của đồ thị hàm số y = g(x) đối với hệ trục toạ độ Oxy?
Giải rút gọn:

a) ![]() và
và ![]() luôn có nghĩa
luôn có nghĩa ![]()
![]() .
.
Vậy TXĐ của hàm số ![]() là
là ![]() và TXĐ của hàm số
và TXĐ của hàm số ![]() là
là ![]() .
.
b) ![]() , có:
, có:
![]()
Vậy ![]() .
.
Đồ thị hàm số ![]() đối xứng với nhau qua trục tung Oy.
đối xứng với nhau qua trục tung Oy.
c) ![]() , có:
, có:
![]()
Vậy ![]() .
.
Đồ thị hàm số ![]() nhận gốc tọa độ O làm tâm đối xứng.
nhận gốc tọa độ O làm tâm đối xứng.
Bài 2: Xét tính chẵn, lẻ của hàm số ![]() .
.
Giải rút gọn:
![]() có nghĩa khi
có nghĩa khi ![]() .
.
=> TXĐ của hàm số ![]() là
là ![]() .
.
Do đó, nếu x thuộc D thì ![]() cũng thuộc TXĐ của D.
cũng thuộc TXĐ của D.
Có: ![]()
Vậy ![]() là hàm số lẻ.
là hàm số lẻ.
Bài 3: So sánh:
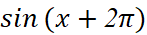 và
và 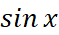 ;
;cos (
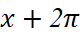 ) và cos
) và cos  ;
;tan (
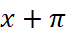 ) và tan
) và tan 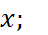
cot (
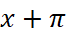 ) và cot
) và cot 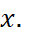
Giải rút gọn:
a) Có: ![]()
![]()
Vậy ![]() .
.
b) Có: ![]()
![]()
Vậy ![]() .
.
c) Có: ![]()
Vậy ![]() .
.
d) Có: ![]()
Vậy ![]() .
.
Bài 4: Hàm số hằng ![]() (c là hằng số) có phải là hàm số tuần hoàn không? Nếu hàm số tuần hoàn thì nó có chu kì không?
(c là hằng số) có phải là hàm số tuần hoàn không? Nếu hàm số tuần hoàn thì nó có chu kì không?
Giải rút gọn:
Hàm số hằng ![]() (c là hằng số) có TXĐ:
(c là hằng số) có TXĐ: ![]()
Với T là số dương bất kì ; ![]() , có:
, có:
+) ![]() và
và ![]()
+) ![]() ( f(x) là hàm số hằng nên với
( f(x) là hàm số hằng nên với ![]() thì giá trị của hàm số đều có giá trị bằng c).
thì giá trị của hàm số đều có giá trị bằng c).
Vậy hàm số hằng f(x) = c (c là hằng số) là hàm số tuần hoàn với chu kì là một số dương bất kì.
Bài 5: Xét tính tuần hoàn của hàm số y = ![]()
Giải rút gọn:
Biểu thức có nghĩa khi:
![]()
![]()
=> ![]() có TXĐ là
có TXĐ là ![]() .
.
Với ![]() số thực , có:
số thực , có:
+) ![]()
+) ![]()
Vậy ![]() là hàm số tuần hoàn với chu kì
là hàm số tuần hoàn với chu kì ![]() .
.
3. ĐỒ THỊ VÀ TÍNH CHẤT CỦA HÀM SỐ Y = SINX
Bài 1: Cho hàm số y = ![]()
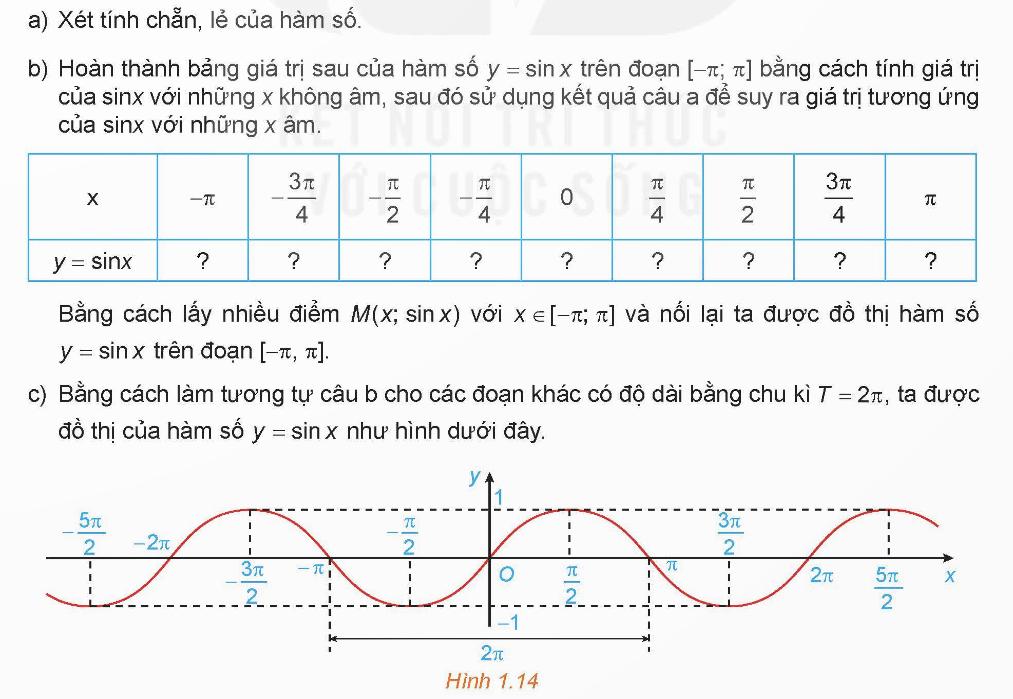
Giải rút gọn:
a) Hàm số ![]() có TXĐ là
có TXĐ là ![]() .
.
Nếu ![]() thì
thì ![]()
Có: ![]()
![]()
Vậy ![]() là hàm số lẻ.
là hàm số lẻ.
b) Có: ![]()
![]()
Vì ![]() là hàm số lẻ nên:
là hàm số lẻ nên:
 ;
; 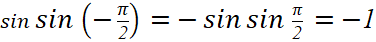 ;
; ;
; .
.
Vậy ta hoàn thành được bảng như sau:
x |
|
|
|
|
| 0 |
|
|
|
x | 0 |
|
|
|
| 0 |
| 1 |
|
x |
| |||
| 0 | |||
c) Đồ thị của hàm số y = sin x :
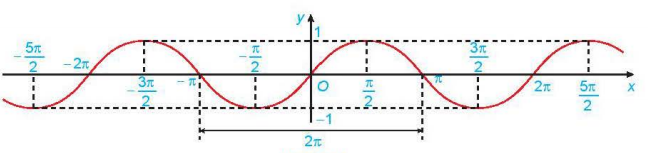
Bài 2: Tập giá trị của hàm số:
Giải rút gọn:
Ta có: ![]() với
với ![]() .
.
Suy ra ![]() .1; hay:
.1; hay:
![]() với
với ![]() .
.
Vậy hàm số ![]() có tập giá trị là
có tập giá trị là ![]() .
.
