Slide bài giảng Toán 11 kết nối Bài 10: Đường thẳng và mặt phẳng trong không gian

Tóm lược nội dung

BÀI 10. ĐƯỜNG THẲNG VÀ MẶT PHẲNG TRONG KHÔNG GIAN

1. KHÁI NIỆM MỞ ĐẦU

Bài 1: Hãy tìm một số hình ảnh mặt phẳng trong thực tế

Giải rút gọn: 

Mặt bàn, mặt gương phẳng, mặt sàn phẳng, trần nhà phẳng,...

Bài 2: Chấm phạt đền trên sân bóng đá cho ta hình ảnh về một điểm thuộc một mặt phẳng. Hãy tìm thêm các ví dụ khác cũng gợi cho ta hình ảnh đó.

Giải rút gọn: 

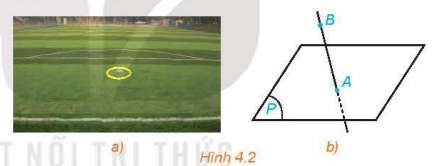
- Một chấm mực trên tờ giấy trắng.

Kết luận:

+ Điểm .

+ Điểm .

Nếu ta còn nối nằm trên , chứa , đi qua .

2. CÁC TÍNH CHẤT THỪA NHẬN

Bài 1: Chiếc xà ngang đặt tựa lên hai điểm A,B của trụ nhảy thể hiện hình ảnh của một đường thẳng đi qua hai điểm đó. Có thể tìm được một đường thẳng khác cũng đi qua hai điểm A, B hay không?

Giải rút gọn: 

Không thể tìm được đường thẳng nào khác 

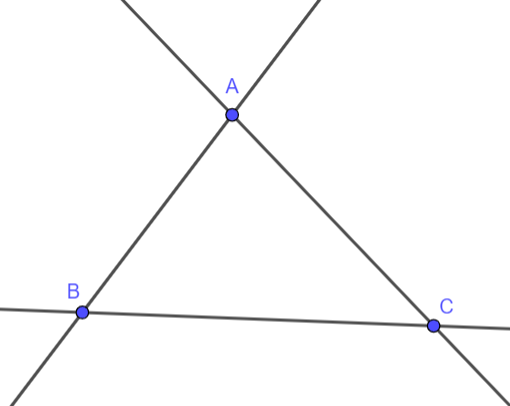
Bài 2: Có bao nhiêu đường thẳng đi qua hai trong số ba điểm không thẳng hàng?

Giải rút gọn: 

+ 3 điểm không thẳng hàng

+ 1 đường thẳng từ 2 trong 3 điểm đó,

=> Khi đó số đường thẳng tạo thành 3 đường thẳng.

Bài 3: Trong Hình 4.4 là một khối rubik có bốn đỉnh và bốn mặt, mỗi mặt là một tam giác.

1. Đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn hay không?
2. Có thể đặt khối rubik sao cho bốn đỉnh của nó đều nằm trên mặt bàn không?

Giải rút gọn: 

a) Khi đặt khối rubik sao cho ba đỉnh của mặt màu đỏ đều nằm trên mặt bàn, mặt màu đỏ của khối rubik nằm trên mặt bàn.

b) Không thể đặt 

Bài 4: Có bao nhiêu mặt phẳng đi qua ba điểm thẳng hàng?

Giải rút gọn: 

• Qua ba điểm thẳng hàng, 

• Một đường thẳng. Có vô số mặt phẳng đi qua đường thẳng này nên có vô số mặt phẳng đi qua ba điểm thẳng hàng.

Bài 5: Cho tứ giác ABCD. Có bao nhiêu mặt phẳng đi qua ba trong bốn đỉnh của tứ giác đó?

Giải rút gọn: 

Vì 4 điểm tạo thành 1 tứ giác tạo thành 1 mặt phẳng duy nhất là mặt phẳng

Vậy có 1 mặt phẳng thỏa mãn yêu cầu bài toán.

Bài 6: Hãy giải thích tại sao trong thực tiễn có nhiều đồ vật được thiết kế gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nồi,...

Giải rút gọn: 

• Có một và chỉ một mặt phẳng đi qua ba điểm không thẳng hàng. 

Do đó, khi thiết kế các đồ vật gồm ba chân như chân đỡ máy ảnh, giá treo tranh, kiềng ba chân treo nổi,... ta thấy các đồ vật này có thể đứng thẳng mà không bị đổ trên các bề mặt bởi vì các ba chân của các đồ vật này giống như 3 điểm không thẳng hàng.

Bài 7: Trong Ví dụ 2, lấy điểm N thuộc đường thẳng AB sao cho N khác M. Đường thẳng MN có thuộc mặt phẳng (ABC) hay không?

Giải rút gọn: 

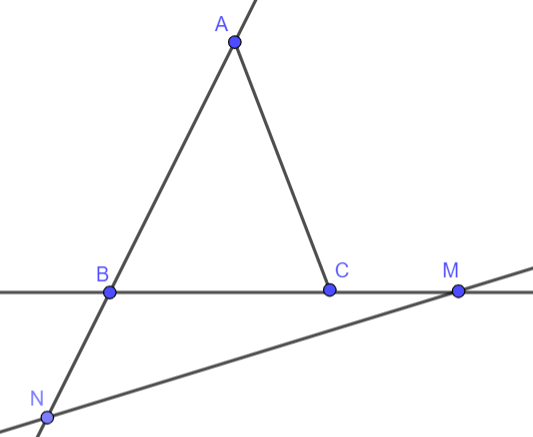
Đường thẳng có hai điểm phân biệt =>  

Vì =>

Khi đó đường thẳng có hai điểm phân biệt =>

Bài 8: Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. Khi đó, sợi dây có nằm trên mặt bàn hay không?

Giải rút gọn: 

Căng một sợi dây sao cho hai đầu của sợi dây nằm trên mặt bàn. 

=> Sợi dây nằm trên mặt bàn.

Bài 9: Trong Hình 4.7, mặt nước và thành bể có giao nhau theo đường thẳng hay không?

Giải rút gọn: 

Mặt nước và thành bể giao nhau theo đường thẳng.

Bài 10: Trong ví dụ 3, hãy xác định giao tuyến của hai mặt phẳng (SBM) và (SCN).

Giải rút gọn: 

Ta có: ∩ = { }

=> , điểm =>  

Vậy là một điểm chung của

Vì S và A là hai điểm chung của nên

3. CÁCH XÁC ĐỊNH MỘT MẶT PHẲNG

Bài 1: Cho đường thẳng a và điểm A không thuộc d. Trên đường thẳng ở lấy hai điểm phân biệt B, C (H.4.9). Mặt phẳng (ABC) có chứa điểm A và đường thẳng ở hay không? Mặt phẳng (ABC) có chứa hai đường thẳng AB và BC hay không?

Giải rút gọn: 

d đi qua hai điểm phân biệt => đường thẳng ; chứa đường thẳng . 

; chứa điểm .

chứa các điểm nên chứa hai đường thẳng và .

CÒN TIẾP…