Slide bài giảng Toán 11 kết nối Bài 12: Đường thẳng và mặt phẳng song song

Tóm lược nội dung

BÀI 12. ĐƯỜNG THẲNG VÀ MẶT PHẲNG SONG SONG

1. ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG

Bài 1: Quan sát hình ảnh khung thành bóng đá và nhận xét vị trí của xà ngang, cột dọc, thanh chống và thanh bên của khung thành với mặt đất.

Giải rút gọn: 

- Xà ngang nằm phía trên và không có điểm chung với mặt đất;

- Cột dọc thẳng đứng và có 1 điểm chung với mặt đất;

- Thanh chống nằm xiên và có 1 điểm chung với mặt đất;

- Thanh bên nằm hoàn toàn trên mặt đất, có vô số điểm chung với mặt đất.

Bài 2: Hãy chỉ ra một hình ảnh đường thẳng song song với mặt phẳng trong bức tranh bên (H.4.34).

Giải rút gọn: 

- Đường thẳng được tạo bởi thanh ngang của cây cầu song song với mặt nước lúc tĩnh lặng.

Bài 3: Trong Ví dụ 1, đường thẳng AC cắt các mặt phẳng nào, nằm trong các mặt phẳng nào?

Giải rút gọn: 

- Đường thẳng cắt các mặt phẳng: và

- Đường thẳng nằm trong mặt phẳng: và

2. ĐIỀU KIỆN VÀ TÍNH CHẤT CỦA ĐƯỜNG THẲNG SONG SONG VỚI MẶT PHẲNG

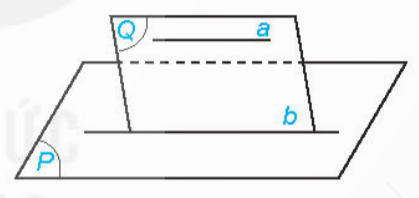
Bài 1: Cho đường thẳng a không nằm trong mặt phẳng (P) và a song song với đường thẳng b nằm trong (P). Gọi (Q) là mặt phẳng chứa a và b (H.4.36).

Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.

Nếu a và (P) cắt nhau tại điểm M thì M có thuộc (Q) và M có thuộc b hay không? Hãy rút ra kết luận sau khi trả lời các câu hỏi trên.

Giải rút gọn: 

- Vì thuộc nên nếu cắt tại , thì thuộc giao tuyến của và

Vậy suy ra thuộc .

- Kết luận: Nếu không nằm trong và song song với thuộc thì song song với hay và không có điểm chung.

Bài 2: Phát biểu trên còn đúng không nếu bỏ điều kiện " không nằm trong mặt phẳng "

Giải rút gọn: 

Phát biểu trên không còn đúng nếu bỏ điều kiện " không nằm trong mặt phẳng ". Vì khi đó, có thể thuộc mặt phẳng .

Bài 3: Trong Ví dụ 2, chứng minh rằng đường thẳng c song song với mp(a, b), đường thẳng b song song với mp(a, c).

Giải rút gọn: 

+) a, b, c không cùng nằm trong một mặt phẳng nên: không thuộc 

Vì và  

=> .

+) a, b, c không cùng nằm trong một mặt phẳng => không thuộc

Vì và => .

Bài 4: Cho hình chóp S.ABCD có đáy là hình thang (AB// CD). Hai đường thẳng SD và AB có chéo nhau hay không? Chỉ ra mặt phẳng chứa đường thẳng SD và song song với AB.

Giải rút gọn: 

+) và chéo nhau.

+) không nằm trong mặt phẳng và (giả thiết), 

, 

Nên

Mà mặt phẳng chứa đường thẳng. Vậy mặt phẳng chứa đường thẳng và // .

CÒN TIẾP…