Slide bài giảng Toán 11 kết nối Bài 15: Giới hạn của dãy số
Slide điện tử Bài 15: Giới hạn của dãy số. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 15. GIỚI HẠN CỦA DÃY SỐ
1. GIỚI HẠN HỮU HẠN CỦA DÃY SỐ
Bài 1: Nhận biết dãy số có giới hạn là 0
Cho dãy số (![]() ) với
) với ![]() =
= ![]() .
.
- Biểu diễn năm số hạng đầu của dãy số này trên trục số.
- Bắt đầu từ số hạng nào của dãy, khoảng cách từ
 đến 0 nhỏ hơn 0,01?
đến 0 nhỏ hơn 0,01?
Giải rút gọn:
a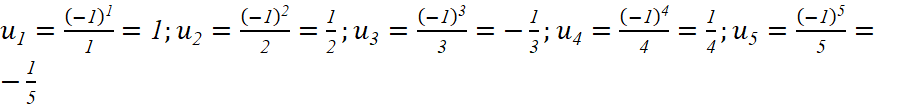
Biểu diễn các số hạng này trên trục số.
![]()
b) Khoảng cách từ ![]() đến 0 :
đến 0 : ![]() .
.
![]()
Vậy bắt đầu từ số hạng thứ 101 của dãy thì khoảng cách từ ![]() đến 0 nhỏ hơn 0,01.
đến 0 nhỏ hơn 0,01.
Bài 2: Chứng minh rằng ![]() = 0
= 0
Giải rút gọn:
![]()
![]() ;
; ![]()
⇒ ![]() .
.
Bài 3: Nhận biết dãy số có giới hạn hữu hạn
Cho dãy số (![]() ) với
) với ![]() =
= ![]() . Xét dãy số (
. Xét dãy số (![]() ) xác định bởi
) xác định bởi ![]()
Giải rút gọn:
![]()
![]()
⇒ ![]()
Bài 4: Cho dãy số (![]() ) với
) với ![]() =
=![]() . Chứng minh rằng
. Chứng minh rằng ![]()
Giải rút gọn:
![]()
![]() khi
khi ![]()
⇒ ![]() .
.
Bài 5: Một quả bóng cao su được thế từ độ cao 5 m xuống một mặt sàn. Sau mỗi lần 2 chạm sàn, quả bóng nảy lên độ cao bằng ![]() độ các trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử (
độ các trước đó. Giả sử rằng quả bóng luôn chuyển động vuông góc với mặt sàn và quá trình này tiếp diễn vô hạn lần. Giả sử (![]() ) là độ cao (tính bằng mét) của quá bóng sau lần này lên thứ n. Chứng minh rằng dãy số (
) là độ cao (tính bằng mét) của quá bóng sau lần này lên thứ n. Chứng minh rằng dãy số (![]() ) со giới hạn là 0.
) со giới hạn là 0.
Giải rút gọn:
Sau lần chạm sàn đầu tiên, quả bóng nảy lên một độ cao: ![]()
Tiếp đó, bóng rơi từ độ cao ![]() xuống mặt sàn và nảy lên độ cao là:
xuống mặt sàn và nảy lên độ cao là:
![]()
Tiếp đó, bóng rơi từ độ cao u2 xuống mặt sàn và nảy lên độ cao là:
![]()
Tiếp tục …
Sau lần chạm sàn thứ n, quả bóng nảy lên độ cao : ![]()
=> ![]() ⇒
⇒ ![]()
2. ĐỊNH LÍ VỀ GIỚI HẠN CỦA DÃY SỐ
Bài 1: Hình thành quy tắc tính giới hạn:
Cho hai dãy số (![]() ) và (
) và (![]() ) với
) với ![]() = 2+
= 2+![]() ,
, ![]() = 3 -
= 3 - ![]() .
.
Tìm và so sánh: ![]() và
và ![]() +
+ ![]() .
.
Giải rút gọn:
![]()
![]() khi
khi ![]()
⇒ ![]()
![]() khi
khi ![]()
⇒ ![]()
![]() khi
khi ![]()
⇒ ![]()
⇒ ![]()
Vậy ![]()
Bài 2: Tìm ![]()
Giải rút gọn:
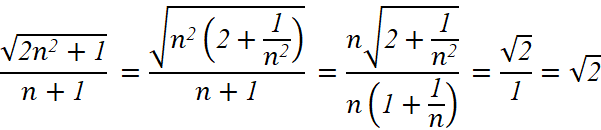
3. TỔNG CỦA CẤP SỐ NHÂN LÙI VÔ HẠN
Bài 1: Làm quen với việc tính tổng vô hạn
Cho hình vuông cạnh 1 (đơn vị độ dài). Chia hình vuông đó thành bốn hình vuông nhỏ bằng nhau, sau đó tô màu hình vuông nhỏ góc dưới bên trái (H.5.2). Lặp lại các thao tác này với hình vuông nhỏ góc trên bên phải. Giả sử quá trình trên tiếp diễn vô hạn lần. Gọi ![]() lần lượt là độ dài canh của các hình vuông được tô màu.
lần lượt là độ dài canh của các hình vuông được tô màu.
- Tính tổng
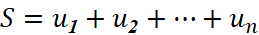
- Tìm S =
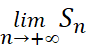 .
.
Giải rút gọn:
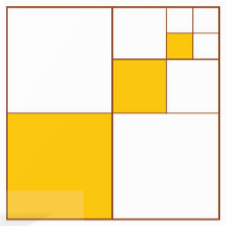
a)
![]() là độ dài cạnh của hình vuông được tô màu tạo từ việc chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau,
là độ dài cạnh của hình vuông được tô màu tạo từ việc chia hình vuông cạnh 1 thành 4 hình vuông nhỏ bằng nhau,
=> ![]() .
.
Tiếp tục: ![]() ,….
,….
=> Độ dài cạnh của các hình vuông được tô màu lập thành một cấp số nhân với ![]() và
và ![]()
⇒ Tổng của n số hạng đầu:
![]()
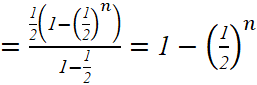
b)
![]()
Bài 2: Tính tổng ![]()
Giải rút gọn:
![]()
Tổng của cấp số nhân lùi vô hạn ![]() ;
; ![]() .
.
⇒ ![]()
Bài 3: (Giải thích nghịch lí Zeno)
Để đơn giản, ta giả sử Achilles chạy với vận tốc ![]() , vận tốc của rùa là
, vận tốc của rùa là ![]() và khoảng cách ban đầu a =
và khoảng cách ban đầu a = ![]() .
.
- Tính thời gian
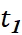 ,
,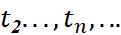 tương ứng để Achilles đi từ
tương ứng để Achilles đi từ 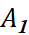 đến
đến 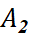 , từ
, từ 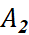 đến
đến 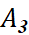 ,..., từ
,..., từ  đến
đến 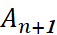 ,...
,... - Tính tổng thời gian cần thiết để Achilles chạy hết các quãng đường
 ,
, 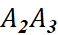 ,...,
,...,  ,..., tức thì là thời gian cần thiết để Achilles đuổi kịp rùa.
,..., tức thì là thời gian cần thiết để Achilles đuổi kịp rùa. - Sai lầm trong lập luận của Zeno là ở đâu?
Giải rút gọn:
![]()
a)
![]() , Achilles phải mất thời gian
, Achilles phải mất thời gian ![]() . Rùa đã chạy được quãng đường
. Rùa đã chạy được quãng đường ![]() .
.
+ ![]() , Achilles phải mất thời gian
, Achilles phải mất thời gian ![]() . Rùa đã chạy được quãng đường
. Rùa đã chạy được quãng đường ![]()
+ ![]() , Achilles phải mất thời gian
, Achilles phải mất thời gian ![]() .
.
b) Tổng thời gian để Achilles chạy hết quãng đường ![]() tức là thời gian cần thiết để Achilles đuổi kịp rùa:
tức là thời gian cần thiết để Achilles đuổi kịp rùa:
![]()
Tổng của một cấp số nhân lùi vô hạn có ![]() và
và ![]() .
.
![]() (giờ)
(giờ)
c) Nghịch lý Zeno chỉ đúng với điều kiện là tổng thời gian Achilles chạy hết các quãng đường để đuổi kịp rùa phải là vô hạn,
Nếu nó hữu hạn thì đó chính là khoảng thời gian mà anh bắt kịp được rùa.
