Slide bài giảng Toán 11 kết nối Bài 4: Phương trình lượng giác cơ bản

Tóm lược nội dung

BÀI 4. PHƯƠNG TRÌNH LƯỢNG GIÁC CƠ BẢN

1. KHÁI NIỆM PHƯƠNG TRÌNH TƯƠNG ĐƯƠNG

Bài 1:Nhận biết khái niệm hai phương trình tương đương:

Cho hai phương trình 2x - 4 = 0 và (x - 2)(x ^ 2 + 1) = 0 

Tìm và so sánh tập nghiệm của hai phương trình trên.

Giải rút gọn: 

* :

Vậy phương trình có tập nghiệm .

*

Vậy phương trình có tập nghiệm .

=> Cả hai phương trình đều có tập nghiệm .

Bài 2: Xét sự tương đương của hai phương trình sau:

và

Giải rút gọn: 

*

+ ĐKXĐ: .

+ (thỏa mãn).

Vậy .

*

+

Vậy

=> Hai phương trình này không phải phương trình tương đương.

2. PHƯƠNG TRÌNH SINX = M

Bài 1: Nhận biết công thức nghiệm của phương trình

a) Quan sát Hình 1.19, tìm các nghiệm của phương trình đã cho trong nửa khoảng [0; 2π).

b) Dựa vào tỉnh tuần hoàn của hàm số sin, hãy viết công thức nghiệm của phương trình đã cho.

Giải rút gọn: 

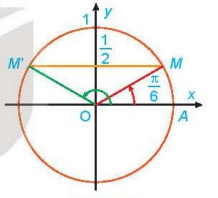
a) lần lượt biểu diễn các góc và , tung độ của điểm M và M' đều = nên theo định nghĩa giá trị lượng giác, có và .

Vậy , có 2 nghiệm là và .

b) Vì hàm số sin có chu kì tuần hoàn là nên phương trình đã cho có công thức nghiệm là: và .

Bài 2: Giải các phương trình sau

Giải rút gọn: 

a)

Vậy phương trình có các nghiệm là và .

b)

.

Vậy phương trình đã cho có các nghiệm là và

3. PHƯƠNG TRÌNH COSX = M

Bài 1: Nhận biết công thức nghiệm của phương trình

Giải rút gọn: 

lần lượt biểu diễn các góc và , lại có hoành độ của điểm và đều bằng  

=> và .

Vậy trong khoảng có hai nghiệm là và

b) Vì hàm số cos có chu kì tuần hoàn là 2π nên phương trình đã cho có công thức nghiệm là và  

Bài 2: Giải các phương trình sau:

b)

Giải rút gọn: 

a)

b)

.

Bài 3:Khi Mặt Trăng quay quanh Trái Đất, mặt đối diện với Trái Đất thường chỉ được Mặt Trời chiếu sáng một phần. Các pha của Mặt Trăng mô tả mức độ phần bề mặt của nó được Mặt Trời chiếu sáng. Khi góc giữa Mặt Trời, Trái Đất và Mặt Trăng là a (0°≤ a ≤ 360°) thì tỉ lệ F của phần Mặt Trăng được chiếu sáng cho bởi công thức

F =

Giải rút gọn: 

a) , có:

Mà  

b) , có:

.

Mà  

c) , có:

. 

Mà  

d) , có:

. 

Mà  

CÒN TIẾP…