Slide bài giảng Toán 11 kết nối Bài 23: Đường thẳng vuông góc với mặt phẳng

Tóm lược nội dung

BÀI 23. ĐƯỜNG THẲNG VUÔNG GÓC VỚI MẶT PHẲNG

1. Đường thẳng vuông góc với mặt phẳng

Bài 1: Đối với cánh cửa như trong Hình 7.10, khi đóng – mở cánh cửa, ta coi mép dưới BC của cánh cửa luôn sát sàn nhà (khe hở không đáng kể).

a) Từ quan sát trên, hãy giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng đi qua B trên sàn nhà.

b) Giải thích vì sao đường thẳng AB vuông góc với mọi đường thẳng trên sàn nhà.

Giải rút gọn: 

a) Đóng - mở cánh cửa:

+ cố định vì luôn đi qua hai bản lề cố định, 

+ trên mặt sàn và luôn qua cố định (là giao của đường thẳng và mặt sàn). 

- Vì quay quanh điểm , => các đường thẳng trên mặt sàn và qua .

b) Lấy đường thẳng bất kì trên mặt sàn. 

Xét là đường thẳng trên mặt sàn, đi qua và // . 

-> .

Bài 2: Nếu đường thẳng Δ và mặt phẳng (P) vuông góc với nhau thì chúng có cắt nhau hay không? 

Giải rút gọn: 

và (P) cắt nhau.

Vì nếu trái lại thì // hoặc nằm trên , 

Tồn tại đường thẳng  

//   

=> , mâu thuẫn với giả thiết .

Bài 3: Gấp tấm bìa cứng hình chữ nhật cứng hình chữ nhật sao cho nếp gấp chia tấm bìa thành hai hình chữ nhật, sau đó đặt nó lên mặt bàn như Hình 7.11.

a) Bằng cách trên, ta tạo được đường thẳng AB vuông góc với hai đường thẳng nào thuộc mặt bàn?

b) Trên mặt bàn, qua điểm A kẻ một đường thẳng a tuỳ ý. Dùng ê ke, hãy kiểm tra trên mô hình xem AB có vuông góc với a hay không.

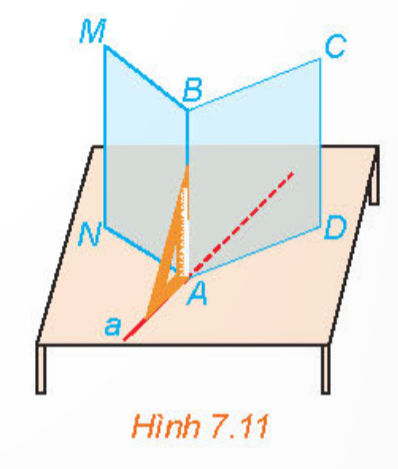
Giải rút gọn: 

a) là các hình chữ nhật =>

b) Đặt ê ke thấy một cạnh của ê ke trùng AB và một cạnh thuộc a nên AB a.

Bài 4: Nếu một đường thẳng vuông góc với hai cạnh của một tam giác thì đường thẳng đó có vuông góc với các cạnh còn lại hay không? 

Giải rút gọn: 

Vì đường thẳng hai cạnh của tam giác nên mặt phẳng chứa tam giác. Nên đường thẳng cạnh thứ ba.

Bài 5: Cho hình chóp S.ABCD có đáy ABCD là hình bình hành tâm O, SA = SC và SB = SD (H.7.14). Chứng minh rằng SO (ABCD).

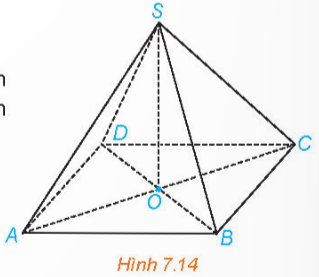
Giải rút gọn: 

Vì và là giao điểm của hai đường chéo AC, BD nên là trung điểm của

CÒN TIẾP…