Slide bài giảng Toán 11 kết nối Bài 24: Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Tóm lược nội dung

BÀI 24. PHÉP CHIẾU VUÔNG GÓC. GÓC GIỮA ĐƯỜNG THẲNG VÀ MẶT PHẲNG

1. Phép chiếu vuông góc. Góc giữa đường thẳng và mặt phẳng

Bài 1: Trên sân phẳng có một cây cột thẳng vuông góc với mặt sân.

 a) Dưới ánh sáng mặt trời, bóng của cây cột trên sân có thể được nhìn như là hình chiều của cây cột qua phép chiếu song song nào không?

b) Khi tia sáng mặt trời vuông góc với mặt sân, liệu ta có thể quan sát được bóng của cây cột trên sân hay không?

Giải rút gọn: 

a) Phép chiếu // theo phương tia sáng mặt trời lên mặt sân.

b) Không thể quan sát.

Bài 2:

a) Nếu A là một điểm không thuộc mặt phẳng (P) và A’ là hình chiếu của A trên (P) thì đường thẳng AA’ có quan hệ gì với mặt phẳng (P)?

b) Nếu đường thẳng a vuông góc với mặt phẳng (P) thì hình chiếu của a trên (P) là gì? 

Giải rút gọn: 

a) vuông góc với mặt phẳng

b) Hình chiếu vuông góc của đường thẳng trên mặt phẳng là một điểm, là giao điểm của và

Bài 3: Cho đường thẳng a và mặt phẳng (P) không vuông góc với nhau. Xét b là một đường thẳng nằm trong (P). Trên a, lấy hai điểm M, N tuỳ ý. Gọi M', N' tương ứng là hình chiếu của M, N trên mặt phẳng (P) (H.7.34).

a) Hình chiếu của a trên mặt phẳng (P) là đường thẳng nào?

b) Nếu b vuông góc với M'N' thì b có vuông góc với a hay không?

c) Nếu b vuông góc với a thì b có vuông góc với M'N' hay không?

Giải rút gọn: 

a) Là đường thẳng

b)

c)

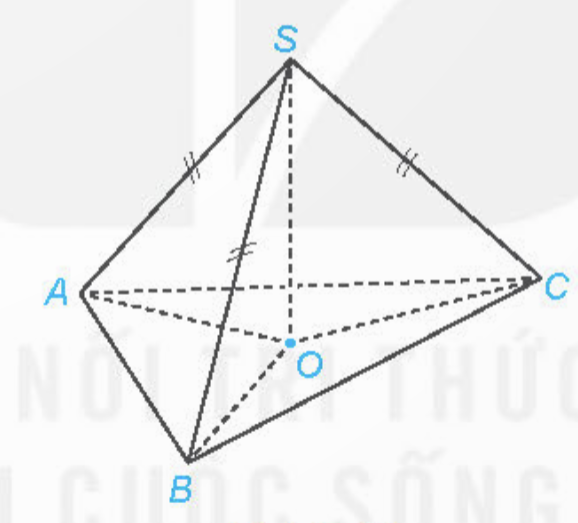
Bài 4: Cho hình chóp S.ABC có SA = SB = SC. Gọi O là hình chiếu của S trên mặt phẳng (ABC) (H.7.36).

a) Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác ABC.

b) Xác định hình chiếu của đường thẳng SA trên mặt phẳng (ABC)

c) Chứng minh rằng nếu AO BC thì SA BC

d) Xác định hình chiếu của các tam giác SBC, SCA, SAB trên mặt phẳng (ABC)

Giải rút gọn: 

a)

->

Vậy O là tâm đường tròn ngoại tiếp tam giác ABC.

b) Hình chiếu của trên mặt phẳng là

c) Do -> , mà

⇒ BC

⇒ .

d) Hình chiếu của mỗi tam giác trên mặt phẳng (ABC) lần lượt là tam giác

2. Góc giữa đường thẳng và mặt phẳng

Bài 1: Một máy bay giữ vận tốc không đổi, với độ lớn 240km/h trong suốt 2 phút đầu kể từ khi cất cánh. Hỏi thông tin trên có đủ để ta xác định độ cao của máy bay so với mặt đất phẳng, tại thời điểm 1 phút kể từ khi máy bay cất cánh không?

Giải rút gọn: 

Thông tin chưa đủ để xác định độ cao.

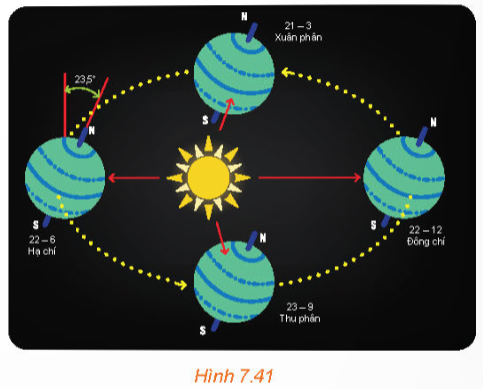
Bài 2: Tâm Trái Đất chuyển động quanh Mặt Trời theo quỹ đạo là một đường elip nhận tâm Mặt Trời làm tiêu điểm. Trong quá trình chuyển động, Trái Đất lại quay quanh trục Bắc Nam. Trục này có phương không đổi và luôn tạo với mặt phẳng chứa quỹ đạo một góc khoảng 66,5°. 

a) Giải thích vì sao hình chiếu của trục Trái Đất trên mặt phẳng quỹ đạo (P) cũng có phương không đổi.

b) Giải thích vì sao có hai thời điểm trong năm mà tại đó hình chiếu của trục Trái Đất trên mặt phẳng (P) thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

Giải rút gọn: 

a) Gọi là một vị trí của trục Trái Đất;

 tương ứng là hình chiếu của trên (P).

Nếu có phương không đổi thì hình chiếu của lên có phương không đổi; nên có phương không đổi.

Gọi là một vị trí trục của Trái Đất khác trục ;

 tương ứng là hình chiếu của trên (P).

Có: có phương khác phương chiếu;

// hoặc và trùng nhau (tính chất phép chiếu song song).

Vậy hình chiếu của trục Trái Đất có phương không đổi.

b) Gọi là đường thẳng đi qua tâm Mặt Trời và có phương là phương chiếu của trục Trái Đất trên (P).

⇒ m có phương không đổi.

Khi đó hình chiếu của trục Trái Đất xuống (P) thuộc đường thẳng m 

⇔ tâm Trái Đất là giao của m với đường elip quỹ đạo của Trái Đất.

Vậy có hai vị trí thuộc quỹ đạo, ứng với hai thời điểm trong năm mà hình chiếu của trục Trái Đất trên (P) thuộc đường thẳng nối tâm Mặt Trời và tâm Trái Đất.

CÒN TIẾP…