Slide bài giảng Toán 11 kết nối Bài 13: Hai mặt phẳng song song

Tóm lược nội dung

BÀI 13. HAI MẶT PHẲNG SONG SONG

1. HAI MẶT PHẲNG SONG SONG

Bài 1: Các mặt bậc thang trong Hình 4.40 gợi nên hình ảnh về các mặt phẳng không có điểm chung. Hãy tìm thêm một số ví dụ khác cũng gợi nên hình ảnh đó.

Giải rút gọn: 

- Các mặt của từng tầng trong giá để dép gợi nên hình ảnh về các mặt phẳng không có điểm chung.

- Mặt sàn và mặt trần nhà bằng gợi nên hình ảnh về các mặt phẳng không có điểm chung.

- Hai mặt đối diện của hộp diêm gợi nên hình ảnh về các mặt phẳng không có điểm chung.

Bài 2: Trong hình ảnh mở đầu, các nhát cắt có nằm trong các mặt phẳng song song hay không?

Giải rút gọn: 

Các nhát cắt nằm trong các mặt phẳng song song.

2. ĐIỀU KIỆN VÀ TÍNH CHẤT CỦA HAI MẶT PHẲNG SONG SONG

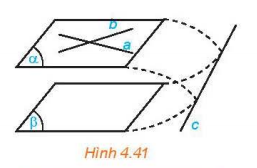
Bài 1: Cho mặt phẳng (a) chứa hai đường thẳng cắt nhau a, b và a, b cùng song song với mặt phẳng (β) (H.4.41).

Nếu (a) và (β) cắt nhau theo giao tuyến c thì hai đường thẳng a và c có song song với nhau hay không, hai đường thẳng b và c có song song với nhau hay không?

Hãy rút ra kết luận sau khi trả lời các câu hỏi trên

Giải rút gọn: 

Do // mặt phẳng và nằm trong mặt phẳng nên và cắt nhau theo giao tuyến // . 

// => a song song với hoặc trùng với .

Bài 2: Nếu không có điều kiện “hai đường thẳng và trùng nhau” thì khẳng định trên còn đúng không?

Giải rút gọn: 

Giả sử và trùng nhau=> trường hợp hai mặt phẳng và cắt nhau theo giao tuyến // hai đường thẳng trùng nhau

=> và không song song với nhau. 

Do vậy, nếu không có điều kiện “hai đường thẳng cắt nhau” thì khẳng định trên không đúng.

Bài 3: Trong không gian cho bốn điểm A, B, C, D không đồng phẳng. Qua điểm A vẽ hai đường thẳng m, n lần lượt song song với hay đường thẳng BC, BD. Chứng minh rằng mp(m, n) song song với mặt phẳng (BCD).

Giải rút gọn: 

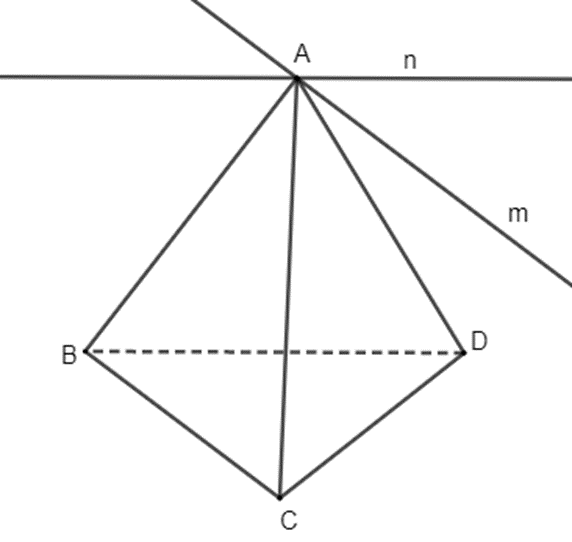
Vì =>

Vì =>

; ;

=>

Bài 4: Một chiếc bàn có phần chân là hai khung sắt hình chữ nhật có thể xoay quanh một trục như trong Hình 4.43. Khi mặt bàn được đặt lên phần chân bàn thì mặt bàn luôn song song với mặt đất. Hãy giải thích tại sao

Giải rút gọn: 

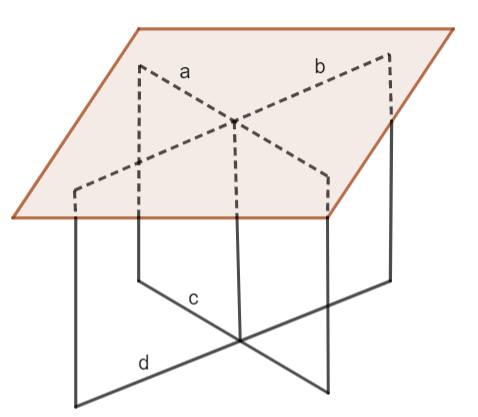
Khung sắt có dạng hình chữ nhật nên các cạnh đối diện của khung sắt // với nhau => và

Vì và là các đường thẳng của chân bàn nằm trên mặt đất,

=> thì đường thẳng // mặt đất và thì đường thẳng // mặt đất.

Mặt phẳng bàn chứa hai đường thẳng cắt nhau và cùng // mặt đất nên mặt phẳng bàn // mặt đất.

Bài 5: Đặt một bìa cứng lên một góc của mặt bàn nằm ngang (H.4.44) sao cho mặt bìa song song với mặt đất. Khi đó mặt bìa song song với mặt đất. Khi đó mặt bìa có trùng với mặt bàn hay không?

Giải rút gọn: 

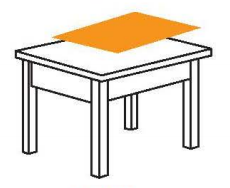
Mặt bàn nằm ngang // mặt đất. 

Khi tấm bìa cứng được đặt lên một góc của mặt bàn nằm ngang sao cho mặt bìa // mặt bàn thì mặt bìa trùng với mặt bàn.

Bài 6: Nếu hai mặt phẳng phân biệt cùng song song  với mặt phẳng thứ ba thì hai mặt phẳng đó có song song với nhau hay không? Vì sao?

Giải rút gọn: 

Có song song với nhau.

Chứng minh: Cho ba mặt phẳng phân biệt có Theo tính chất bắc cầu ta có

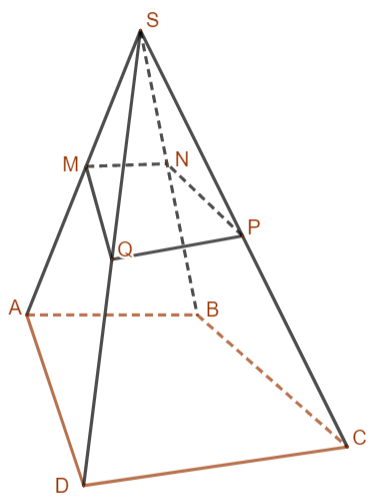
Bài 7: Cho hình chóp S.ABCD. Gọi M, N, P, Q lần lượt là trung điểm của các cạnh SA, SB, SC, SD (H.4.45). Chứng minh rằng hai mặt phẳng (MNP) và (NPQ) cùng song song với mặt phẳng (ABCD), từ đó suy ra bốn điểm M, N, P, Q đồng phẳng.

Giải rút gọn: 

Xét có hay

=> (theo định lí Thalès).

=>   

Tương tự, nên  

Vậy chứa hai đường thẳng cắt nhau và cùng song song với  

=>  

và cùng đi qua điểm và => hai mặt phẳng đó trùng nhau, tức là bốn điểm đồng phẳng.

Bài 8: Cho hai mặt phẳng song song (P) và (Q). Giả sử mặt phẳng (R) cắt mặt phẳng (P) theo giao tuyến a (H.4.46).

a) Giải thích vì sao mặt phẳng (R) cắt mặt phẳng (Q).

b) Gọi b là giao tuyến của hai mặt phẳng (R) và (Q). Hai đường thẳng a và b có thể chéo nhau hay không, có thể cắt nhau hay không?

Giải rút gọn: 

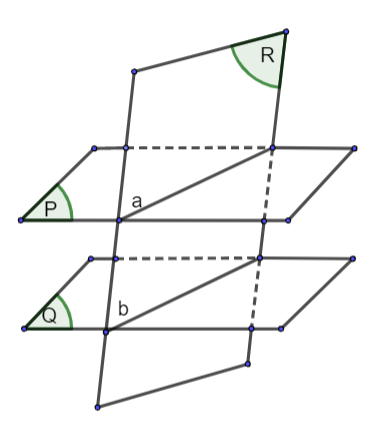
(hình 4.46)

a) Giả sử:

không cắt => . 

  => . Điều này mâu thuẫn với giả thiết

b) Vì => không thể chéo nhau.

=> không có điểm chung.

Giả sử: có điểm chung là => cũng có điểm chung là . Điều này mâu thuẫn với giả thiết

CÒN TIẾP…