Slide bài giảng Toán 11 kết nối Bài 20: Hàm số mũ và hàm số lôgarit
Slide điện tử Bài 20: Hàm số mũ và hàm số lôgarit. Trình bày với các hiệu ứng hiện đại, hấp dẫn. Giúp học sinh hứng thú học bài. Học nhanh, nhớ lâu. Có tài liệu này, hiệu quả học tập của học môn Toán 11 Kết nối tri thức sẽ khác biệt
Bạn chưa đủ điều kiện để xem được slide bài này. => Xem slide bài mẫu
Tóm lược nội dung
BÀI 20. HÀM SỐ MŨ VÀ HÀM SỐ LÔGARIT
1. Hàm số mũ
Bài 1:
a) Tính ![]() khi x lần lượt nhân các giá trị -1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của y =
khi x lần lượt nhân các giá trị -1; 0; 1. Với mỗi giá trị của x có bao nhiêu giá trị của y =![]() tương ứng?
tương ứng?
b) Với những giá trị nào của x, biểu thức y = ![]() có nghĩa?
có nghĩa?
Giải rút gọn:
a)
- Với
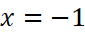 thì
thì 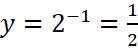
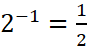 .
. - Với
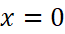 thì
thì 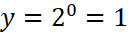
- Với
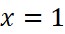 thì
thì 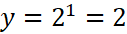
b) Có nghĩa với mọi giá trị của ![]()
Bài 2: Trong các hàm số sau, những hàm số nào là hàm số mũ? Khi đó hãy chỉ ra cơ số.
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Giải rút gọn:
a) là hàm số mũ có cơ số là ![]() .
.
b) là hàm số mũ có cơ số là ![]()
c) là hàm số mũ có cơ số là ![]() .
.
d) không là hàm số mũ.
Bài 3: Cho hàm số mũ ![]()
a)
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| ? | ? | ? | ? | ? | ? | ? |
b) Biểu diễn các điểm (x; y) trong bảng giá trị.
Bằng cách làm tương tự, lấy nhiều điểm (x; ![]() ) với x∈R
) với x∈R
-> nối lại ta được đồ thị của hàm số y =![]()
c) Tập giá trị và tính chất biến thiên của hàm số y = ![]()
Giải rút gọn:
a)
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| 0,125 | 0,25 | 0,5 | 1 | 2 | 4 | 8 |
b)
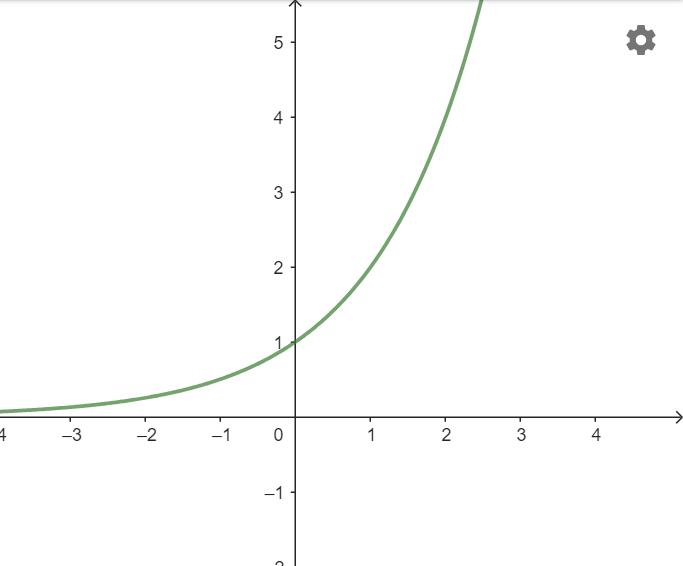
c) Tập giá trị: ![]()
Tính chất biến thiên:
+ Hàm số đồng biến / ![]()
+ Hàm số liên tục / ![]()
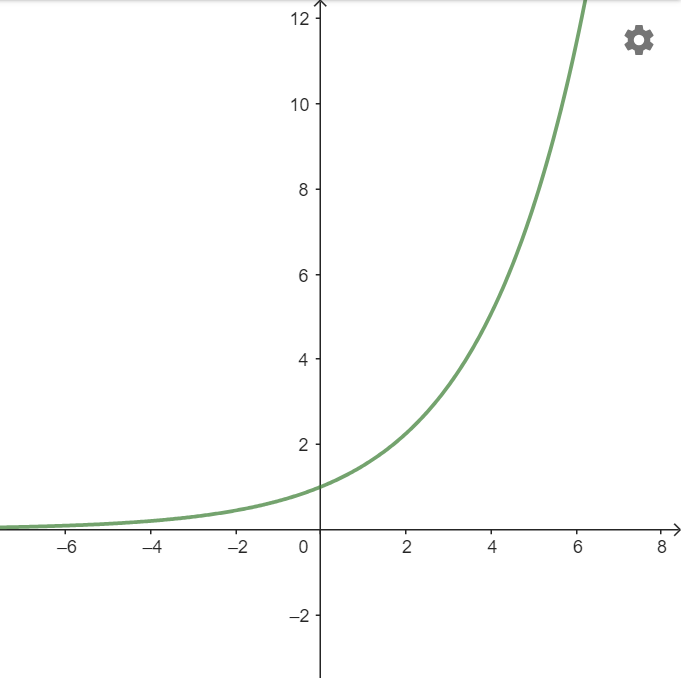
Bài 4: Vẽ đồ thị của hàm số y= ![]()
Giải rút gọn:
2. Hàm số lôgarit
Bài 1:
a) Tính y =![]() khi x lần lượt nhân các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của y =
khi x lần lượt nhân các giá trị 1; 2; 4. Với mỗi giá trị của x > 0 có bao nhiêu giá trị của y =![]() tương ứng?
tương ứng?
b) Với những giá trị nào của x, biểu thức y = ![]() có nghĩa?
có nghĩa?
Giải rút gọn:
a)
+ ![]() thì
thì ![]()
+ ![]() thì
thì ![]()
+ ![]() thì
thì ![]()
b) ![]() có nghĩa khi
có nghĩa khi ![]() .
.
Bài 2: Trong các hàm số sau, những hàm số nào là hàm số lôgarit? Khi đó hãy chỉ ra cơ số.
a) ![]() b)
b) ![]() c)
c) ![]() d)
d) ![]()
Giải rút gọn:
a) ![]() là hàm số lôgarit có cơ số
là hàm số lôgarit có cơ số ![]() .
.
b) ![]() ; là hàm số lôgarit có cơ số
; là hàm số lôgarit có cơ số ![]() .
.
c) ![]() không là hàm số lôgarit.
không là hàm số lôgarit.
d) ![]() không hàm số lôgarit.
không hàm số lôgarit.
Bài 3: Cho hàm số lôgarit ![]()
a)Hoàn thành bảng giá trị sau:
|
|
|
| 1 | 2 |
|
|
| ? | ? | ? | ? | ? | ? | ? |
b) Trong mặt phẳng toạ độ Oxy, biểu diễn các điểm (x, y) trong bảng giá trị ở câu a. Bằng cách làm tương tự, lấy nhiều điểm (x; ![]() ) và nồi lại ta được đồ thị của hàm số y =
) và nồi lại ta được đồ thị của hàm số y = ![]()
c) Từ đồ thị đã vẽ ở câu b, hãy kết luận về tập giá trị và tính chất biến thiên của hàm số y = ![]()
Giải rút gọn:
a)
|
|
|
| 1 | 2 |
|
|
| -3 | -2 | -1 | 0 | 1 | 2 | 3 |
b) ![]()
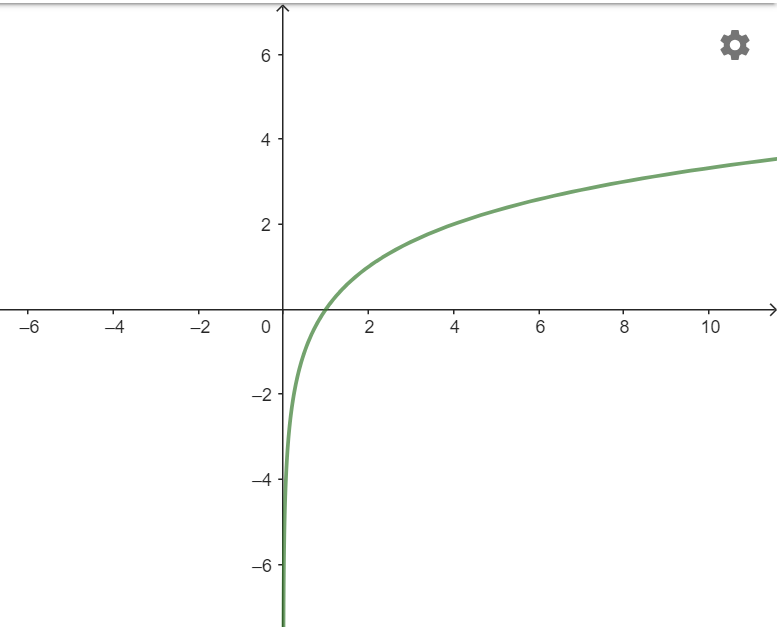
c) Tập giá trị: ![]()
Tính chất biến thiên:
+ Hàm số đồng biến trên ![]()
+ Hàm số liên tục trên ![]()
Bài 4: Giải bài toán tình huống mở đầu (kết quả tính theo đơn vị triệu người và làm tròn đến chữ số thập phân thứ hai).
Giải rút gọn:
2020 đến 2050 : 30 năm.
Ước tính dân số Việt Nam vào năm 2050: ![]() (triệu người)
(triệu người)
3. Bài tập
Bài 6.15: Vẽ đồ thị của các hàm số sau
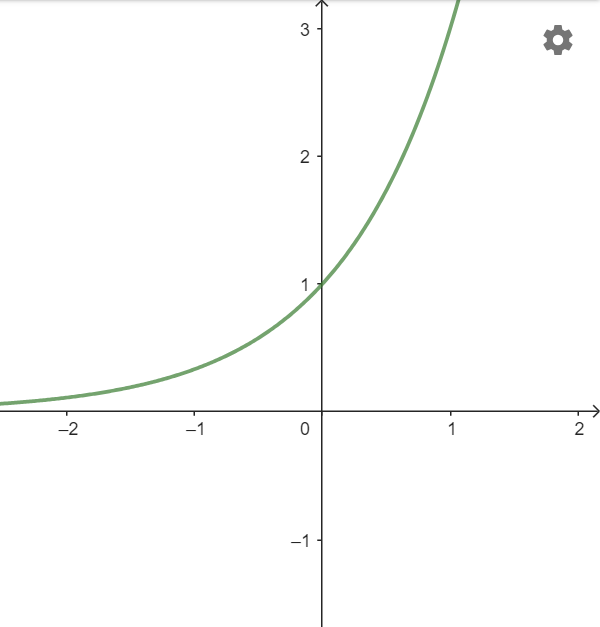
a) ![]()
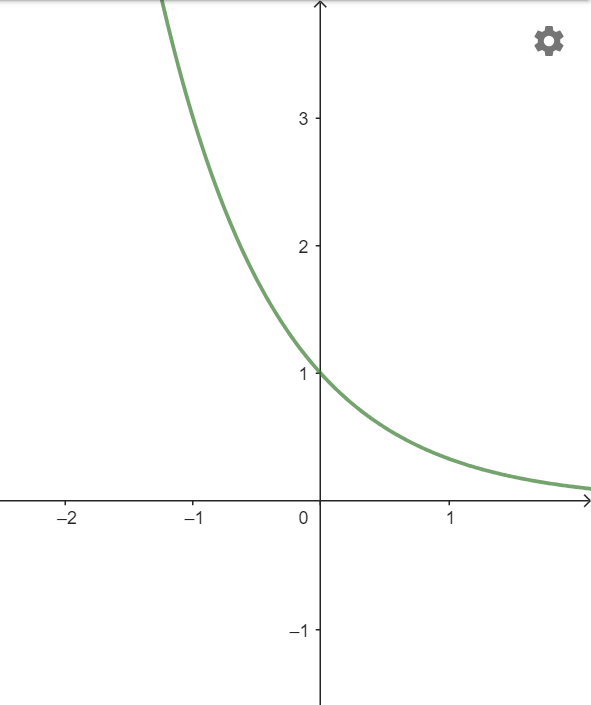
b) ![]()
Giải rút gọn:
a) ![]()
b) ![]()
Bài 6.16: Vẽ đồ thị của các hàm số sau…
a) y= ![]() b) y=
b) y= ![]()
Giải rút gọn:
a)
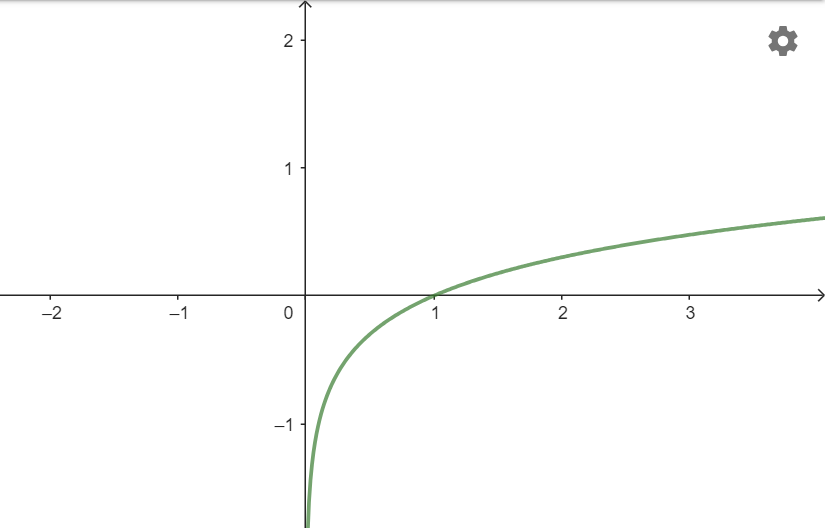
b)
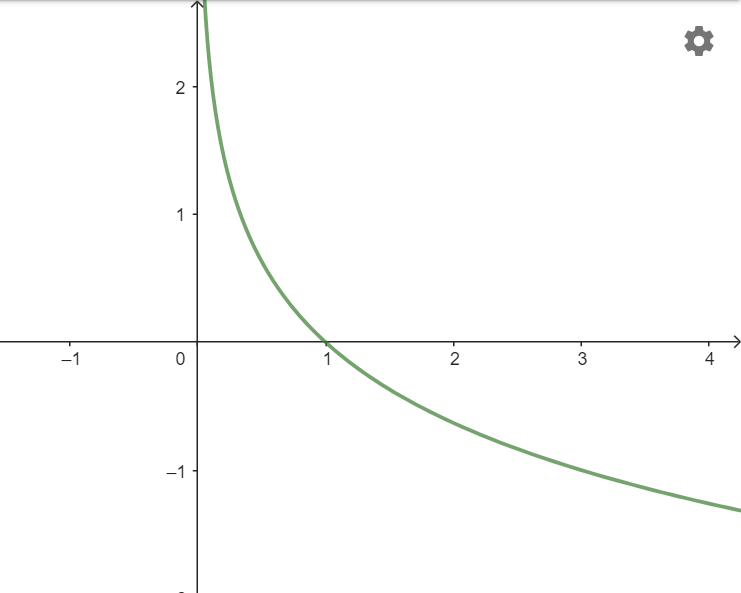
Bài 6.17: Tìm tập xác định của các hàm số sau
y= log
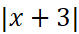 b) y= In(
b) y= In(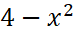 )
)
Giải rút gọn:
a) Điều kiện xác định: ![]() .
.
Vậy tập xác định của hàm số là ![]() .
.
b) Điều kiện xác định: ![]() .
.
Vậy tập xác định của hàm số là ![]() .
.
Bài 6.18: Giả sử một chất phóng xạ bị phân rã theo cách sao cho khối lượng m(t) của chất còn lại (tính bằng kilôgam) sau t ngày được cho bởi hàm số m(t) = 13![]()
a) Tìm khối lượng của chất đó tại thời điểm t= 0.
b) Sau 45 ngày khối lượng chất đó còn lại là bao nhiêu?
Giải rút gọn:
a) Khối lượng của chất tại ![]() là
là
![]()
b) Khối lượng của chất tại ![]() ngày là
ngày là
![]()
Bài 6.19: Trong một nghiên cứu, một nhóm học sinh được cho xem cùng một danh sách các loài động vật và được kiểm tra lại xem họ còn nhớ bao nhiêu phần trăm danh sách đó sau mỗi tháng. Giả sử sau 1 tháng, khả năng nhớ trung bình của nhóm học sinh đó được tính theo công thức M(t) = 75-20ln(t + 1), 0≤ t ≤12 (đơn vị: %). Hãy tính khả năng nhớ trung bình của nhóm học sinh đó sau 6 tháng.
Giải rút gọn:
Khả năng nhớ trung bình của nhóm học sinh sau 6 tháng là
![]()
