Giải câu 6 trang 103 sách phát triển năng lực toán 7 tập 1
6. Cho hình 6.7:
a. Chứng minh Bx // Cy (Gợi ý: Qua A vẽ tia Az song song với Bx).
b. Nhận xét mối quan hệ của ba góc $\widehat{xBA}$ ; $\widehat{BAC}$ và $\widehat{ACy}$ (Gợi ý: Xét tổng ba góc).
c. Liệu có phải với ba góc bất kì có mối quan hệ trên thì Bx // Cy? Vẽ hình minh họa để kiểm chứng.
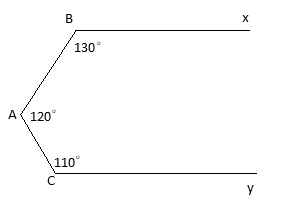
d. Trình bày chứng minh của em cho nhận định tổng quát sau:
Nếu $\widehat{xBA} + \widehat{BAC} + \widehat{ACy} = 360^{\circ}$ thì Bx // Cy.
a.
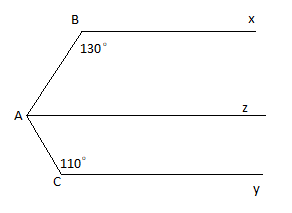
Qua A vẽ tia Az song song với Bx như hình vẽ.
Xét hai góc trong cùng phía $\widehat{xBA}$ và $\widehat{BAz}$ có: $\widehat{xBA}$ + $\widehat{BAz}$ = 180$^{\circ}$
$\Rightarrow \widehat{BAz} = 180^{\circ} - \widehat{xBA} = 180^{\circ} - 130^{\circ} = 50^{\circ}$
Lại có: $\widehat{CAz}$ + $\widehat{BAz}$ = $\widehat{BAC}$
$\Rightarrow \widehat{CAz} = \widehat{BAC} - \widehat{BAz} = 120^{\circ} - 50^{\circ} = 70^{\circ}$
Xét hai góc trong cùng phía $\widehat{CAz}$ và $\widehat{ACy}$ có: $\widehat{CAz}$ + $\widehat{ACy}$ = $70^{\circ} + 110^{\circ} = 180^{\circ} $
Vậy Cy // Az.
Mà Az // Bx
Từ đó suy ra Bx // Cy
b. Mối quan hệ giữa ba góc $\widehat{xBA}$ ; $\widehat{BAC}$ và $\widehat{ACy}$:
$\widehat{xBA} + \widehat{BAC} + \widehat{ACy}$ = $360^{\circ} $
c. Với ba góc bất kì có mối quan hệ trên thì ta có Bx // Cy
d.

Qua A dựng tia Az // Bx như hình vẽ.
Suy ra $\widehat{ABx}$ + $\widehat{BAz}$ = $180^{\circ} $ (*)
Mà $\widehat{CAz}$ + $\widehat{BAz}$ = $\widehat{BAC}$ (**)
Theo đề bài ta có: $\widehat{xBA} + \widehat{BAC} + \widehat{ACy}$ = $360^{\circ} $ (***)
Từ (*), (**) và (***) ta có:
$\widehat{xBA} + \widehat{CAz} + \widehat{BAz} + \widehat{ACy}$ = $360^{\circ} $
$\Leftrightarrow (\widehat{xBA} + \widehat{BAz}) + (\widehat{CAz} +\widehat{ACy})$ = $360^{\circ} $
$\Leftrightarrow 180^{\circ} + (\widehat{CAz} +\widehat{ACy})$ = $360^{\circ} $
$\Leftrightarrow \widehat{CAz} +\widehat{ACy} = 180^{\circ} $
Mà $\widehat{CAz}$ và $\widehat{ACy}$ ở vị trí so le trong nên Cy // Az
Cy // Az và Bx // Az nên ta có: Bx // Cy (đ.p.c.m)

Bình luận