A. LÝ THUYẾT

1. Ở hình 1.1, hai đường thẳng MN và PQ cắt nhau tại K tạo ra bốn góc K₁; K₂; K₃; K₄. Xét cặp góc K₁; K₃ có các cặp cạnh KM; KN và KQ; KP là các tia đối nhau. Tương tự, cặp góc K₂; K₄ có các cặp cạnh KM; KN và KP; KQ là các tia đối nhau. Ta gọi các cặp góc K₁; K₃ và K₂; K₄ là hai góc đối đỉnh.

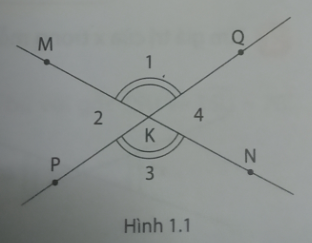
Điền cụm từ thích hợp để hoàn thành định nghĩa sau:

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là ...................... một cạnh của góc kia.

Hướng dẫn:

Hai góc đối đỉnh là hai góc mà mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

Trong những hình dưới đây, hình nào cho ta hai góc đối đỉnh? Nếu không, em hãy đưa ra lí giải của mình.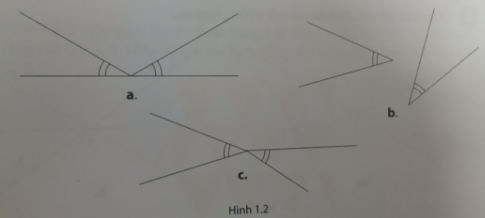

Hướng dẫn:

Trong các hình trên, không có hình nào cho ta hai góc đối đỉnh. Vì trong cả ba hình, cạnh của góc này không là tia đối của một cạnh của góc kia.

2. Tính chất của hai góc đối đỉnh

Sử dụng một tờ giấy trắng và gấp tờ giấy hai lần sao cho nếp gấp thứ hai cắt nếp gấp thứ nhất tại điểm E.

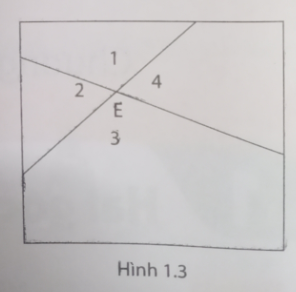
a. Cho biết các cặp góc E₁; E₃ và E₂; E₄ có đối đỉnh hay không? Giải thích.

b. Sử dụng thước đo độ đo các góc E₁; E₂; E₃; E₄. Cho biết mối liên hệ giữa các cặp góc E₁; E₃ và E₂; E₄

c. Hãy thử gấp lại tờ giấy theo các nếp gấp khác nhau để kiểm chứng mối quan hệ thu được từ câu b. Từ đó, em có nhận xét gì về số đo của hai góc đối đỉnh?

Hướng dẫn:

a. Các cặp góc E₁; E₃ và E₂; E₄ đối đỉnh. Vì mỗi cặp góc, mỗi cạnh của góc này là tia đối của một cạnh của góc kia.

b. Học sinh tự đo góc. Và đưa ra kết luận các góc E₁; E₃ bằng nhau và E₂; E₄ bằng nhau.

c. Nhận xét: Hai góc đối đỉnh thì bằng nhau.

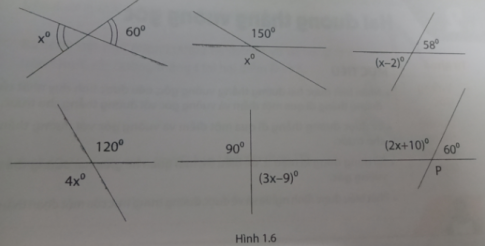
3. Tìm giá trị của x trong mỗi trường hợp sau:

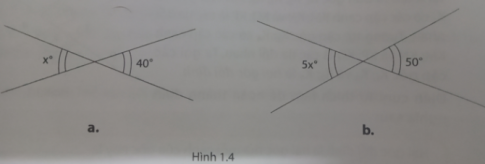
Hướng dẫn:

a. Hai góc trong hình là hai góc đối đỉnh nên x = 40

b. Hai góc trong hình là hai góc đối đỉnh nên 5x = 50 suy ra x = 10.