A. LÝ THUYẾT

1. Trong cuộc sống có nhiều câu dạng điều kiện như:

- Nếu bạn chăm chỉ học hành thì bạn sẽ tích lũy được nhiều tri thức.

- Nếu đun nước lên đến 100$^{\circ}$C thì nước sẽ sôi.

Em hãy chuyển một số nhận xét dưới đây thành dạng câu điều kiện như vậy:

- "Hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau".

- "Hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau".

Một khẳng định suy ra từ những khẳng định khác được coi là đúng thì ta gọi là một định lí. Khi định lí được phát biểu dưới dạng "Nếu ... thì ...", phần nằm giữa từ "Nếu" và từ "thì" là phần giả thiết, phần sau từ "thì" là phần kết luận.

Hướng dẫn:

- "Nếu hai đường thẳng phân biệt cùng vuông góc với một đường thẳng thứ ba thì chúng song song với nhau".

- "Nếu hai đường thẳng phân biệt cùng song song với đường thẳng thứ ba thì chúng song song với nhau".

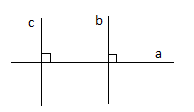
2. Dựa vào hình vẽ bên dưới em hãy cho biết câu điều kiện tương ứng. Viết lại giả thiết và kết luận dưới dạng kí hiệu.

Hình vẽ	Nếu ... thì ...	Giả thiết	Kết luận

Hướng dẫn:

Hình vẽ	Nếu ... thì ...	Giả thiết	Kết luận
	Nếu đường thẳng c cắt đường thẳng a và b trong các góc tạo thành có hai góc so le trong bằng nhau thì đường thẳng a song song với đường thẳng b	đường thẳng c cắt đường thẳng a và b trong các góc tạo thành có hai góc so le trong bằng nhau	đường thẳng a song song với đường thẳng b
	Nếu hai đường thẳng b và c cùng vuông góc với đường thẳng a thì đường thẳng b song song với đường thẳng c.	hai đường thẳng b và c cùng vuông góc với đường thẳng a	đường thẳng b song song với đường thẳng c
	Nếu đường thẳng c vuông góc với đường thẳng a và đường thẳng a song song với đường thẳng b thì đường thẳng c vuông góc với đường thẳng b.	đường thẳng c vuông góc với đường thẳng a và đường thẳng a song song với đường thẳng b	đường thẳng c vuông góc với đường thẳng b.

3. Xét định lí sau: "Hai tia phân giác của hai góc kề bù thì vuông góc với nhau".

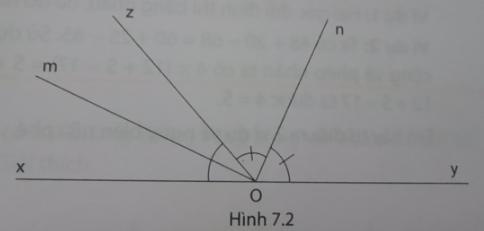
Em hãy viết định lí trên dưới dạng câu điều kiện.

Để chứng minh định lí ta cần dùng lập luận để từ giả thiết suy ra kết luận. Hãy hoàn thành chứng minh định lí trên bằng cách điền vào chỗ chấm một cách thích hợp.

Vì Om là tia phân giác của góc xOz nên $\widehat{mOz}$ = ...   (1)

Vì On là tia phân giác của góc zOy nên $\widehat{zOn}$ = ...   (2)

Từ (1) và (2) ta có:

$\widehat{mOz}$ + $\widehat{zOn}$ = ...    (3)

Mặt khác, $\widehat{xOz}$ và $\widehat{zOy}$ là hai góc kề bù (theo giả thiết) nên từ (3) ta có:

$\widehat{mOn}$ = ... hay $\widehat{mOn}$ = ...

Hướng dẫn:

Vì Om là tia phân giác của góc xOz nên $\widehat{mOz}$ = $\frac{1}{2}$$\widehat{xOz}$   (1)

Vì On là tia phân giác của góc zOy nên $\widehat{zOn}$ = $\frac{1}{2}$$\widehat{zOy}$   (2)

Từ (1) và (2) ta có:

$\widehat{mOz}$ + $\widehat{zOn}$ = $\frac{1}{2}$($\widehat{xOz}+$\widehat{zOy}$)    (3)

Mặt khác, $\widehat{xOz}$ và $\widehat{zOy}$ là hai góc kề bù (theo giả thiết) nên từ (3) ta có:

$\widehat{mOn}$ = $\frac{1}{2}$.$180^{\circ}$ hay $\widehat{mOn}$ = $90^{\circ}$