Giải phát triển năng lực toán 7 BÀI TẬP TỔNG HỢP ÔN TẬP CHƯƠNG II
Giải bài BÀI TẬP TỔNG HỢP ÔN TẬP CHƯƠNG II - Sách phát triển năng lực trong môn toán 7 tập 1 trang 78. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. LÝ THUYẾT
I. Viết tiếp vào chỗ chấm để hoàn thiện các nội dung sau:
1. Đại lượng tỉ lệ thuận. Đại lượng tỉ lệ nghịch
| Đại lượng tỉ lệ thuận | Đại lượng tỉ lệ nghịch | |
| Định nghĩa | Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx, với k là hằng số khác 0 thì ta nói .................. | Nếu đại lượng y liên hệ với đại lượng x theo công thức y = $\frac{a}{x}$, với a là hằng số khác 0 thì ta nói ............ |
| Chú ý | Nếy y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x ............ ........... với y theo hệ số tỉ lệ ................ | Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x ................. với y theo hệ số tỉ lệ ............. |
....... hai giá trị tương ứng của chúng luôn không đổi $\frac{y_{1}}{x_{1}}=\frac{y_{2}}{x_{2}}=\frac{y_{3}}{x_{3}}=...=k$ | ................. hai giá trị tương ứng của chúng luôn không đổi $x_{1}y_{1}=x_{2}y_{2}=x_{3}y_{3}$ = ... = a | |
| Tính chất | Tỉ số hai giá trị bất kì của đại lượng này .................. hai giá trị tương ứng của đại lượng kia $\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}; \frac{x_{2}}{x_{3}}=\frac{y_{2}}{y_{3}};$ ... | Tỉ số hai giá trị bất kì của đại lượng này .................. hai giá trị tương ứng của đại lượng kia $\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}; \frac{x_{1}}{x_{3}}=\frac{y_{3}}{y_{1}};$ ... |
| Chia tỉ lệ | Nếu x, y, z tỉ lệ thuận với a. b, c thì ta có: $\frac{x}{a}$ = ... = ... | Nếu x, y, z tỉ lệ nghịch với a, b, c ta có: ax = ... = ... hay $\frac{x}{\frac{1}{a}}$ = ... = ... |
Hướng dẫn:
| Đại lượng tỉ lệ thuận | Đại lượng tỉ lệ nghịch | |
| Định nghĩa | Nếu đại lượng y liên hệ với đại lượng x theo công thức y = kx, với k là hằng số khác 0 thì ta nói y tỉ lệ thuận với x theo hệ số tỉ lệ k. | Nếu đại lượng y liên hệ với đại lượng x theo công thức y = $\frac{a}{x}$, với a là hằng số khác 0 thì ta nói y tỉ lệ nghịch với x theo hệ số tỉ lệ a. |
| Chú ý | Nếy y tỉ lệ thuận với x theo hệ số tỉ lệ k thì x tỉ lệ thuận với y theo hệ số tỉ lệ $\frac{1}{k}$ | Nếu y tỉ lệ nghịch với x theo hệ số tỉ lệ a thì x tỉ lệ nghịch với y theo hệ số tỉ lệ a. |
Tỉ số hai giá trị tương ứng của chúng luôn không đổi $\frac{y_{1}}{x_{1}}=\frac{y_{2}}{x_{2}}=\frac{y_{3}}{x_{3}}=...=k$ | Tích hai giá trị tương ứng của chúng luôn không đổi $x_{1}y_{1}=x_{2}y_{2}=x_{3}y_{3}$ = ... = a | |
| Tính chất | Tỉ số hai giá trị bất kì của đại lượng này bằng tỉ số hai giá trị tương ứng của đại lượng kia $\frac{x_{1}}{x_{2}}=\frac{y_{1}}{y_{2}}; \frac{x_{2}}{x_{3}}=\frac{y_{2}}{y_{3}};$ ... | Tỉ số hai giá trị bất kì của đại lượng này bằng nghịch đảo của tỉ số hai giá trị tương ứng của đại lượng kia $\frac{x_{1}}{x_{2}}=\frac{y_{2}}{y_{1}}; \frac{x_{1}}{x_{3}}=\frac{y_{3}}{y_{1}};$ ... |
| Chia tỉ lệ | Nếu x, y, z tỉ lệ thuận với a. b, c thì ta có: $\frac{x}{a}$ = $\frac{y}{b}$ = $\frac{z}{c}$ | Nếu x, y, z tỉ lệ nghịch với a, b, c ta có: ax = by = cz hay $\frac{x}{\frac{1}{a}}$ = $\frac{y}{\frac{1}{b}}$ = $\frac{z}{\frac{1}{c}}$ |
2. Đồ thị của hàm số y = ax ($a\neq 0$)
Đồ thị của hàm số y = ax ($a\neq 0$) là một .........................................
Cách vẽ đồ thị hàm số y = ax ($a\neq 0$):
- Vẽ hệ trục tọa độ Oxy.
- Chọn một điểm A(xA; yA) .........................
- ...................... là đồ thị hàm số y = ax ($a\neq 0$).
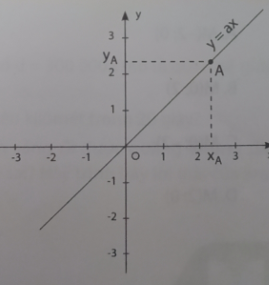
Hướng dẫn:
Đồ thị của hàm số y = ax ($a\neq 0$) là một đường thẳng.
Cách vẽ đồ thị hàm số y = ax ($a\neq 0$):
- Vẽ hệ trục tọa độ Oxy.
- Chọn một điểm A(xA; yA) thuộc đồ thị
- Đường thẳng OA là đồ thị hàm số y = ax ($a\neq 0$).
II. Chọn phương án đúng
1. Đại lượng y tỉ lệ thuận với đại lượng x theo hệ số tỉ lệ là 3. Khi x = 2 thì y bằng:
A. 3
B. 2
C. 5
D. 6
Hướng dẫn:
y = 3x = 3.2 = 6. Chọn D
2. Cho biết hai đại lượng x và y tỉ lệ thuận với nhau và khi x = 3 thì y = 6. Hệ số tỉ lệ k của y đối với x là:
A . 18
B. 2
C. 1/2
D. 3
Hướng dẫn:
k = $\frac{y}{x}= \frac{6}{3}$ = 2. Chọn B
3. x và y là hai đại lượng tỉ lệ nghịch và khi x = 10 thì y = 6. Hệ số tỉ lệ là:
A. 5/3
B. 3/5
C. 60
D. Kết quả khác
Hướng dẫn:
a = x.y = 10.6=60. Chọn C
4. Cho x và y là hai đại lượng thỏa mãn $y = \frac{1}{3x}$. Khẳng định nào sau đây đúng?
A. x và y tỉ lệ nghịch theo hệ số tỉ lệ là 3.
B. x và y tỉ lệ nghịch theo hệ số tỉ lệ là $ \frac{1}{3}$
C. x và y tỉ lệ thuận theo hệ số tỉ lệ là $ \frac{1}{3}$
D. x và tỉ lệ thuận theo hệ số tỉ lệ là 3
Hướng dẫn:
$y = \frac{1}{3x}$ suy ra x.y = $\frac{1}{3}$ hay x và y tỉ lệ nghịch theo hệ số tỉ lệ $\frac{1}{3}$. Chọn B
5. Cho hàm số y = f(x) = -2x - 3. Giá trị của f(-$\frac{1}{2}$) là:
A. 4
B. -4
C. 2
D. -2
Hướng dẫn:
f(-$\frac{1}{2}$) = -2.(-$\frac{1}{2}$) - 3 = 1 - 3 = -2. Chọn D
6. Nếu điểm A có hoành độ bằng 2, tung độ bằng 5 thì tọa độ điểm A là:
A. A(5; 2)
B. A(2; 5)
C. A(2; 2)
D. A(5; 5)
Hướng dẫn:
A(2; 5). Chọn B
7. Điểm (-3; 2) thuộc đồ thị hàm số nào sau đây?
A. y = -6x
B. y = $-\frac{2}{3}$x
C. y = $-\frac{3}{2}$x
D. y = 6x
Hướng dẫn:
$\frac{y}{x}=\frac{2}{-3}\Rightarrow y = \frac{-2}{3}x$. Chọn B.
8. Cho hệ tọa độ Oxy (hình 8.2). Điểm M có tọa độ là:
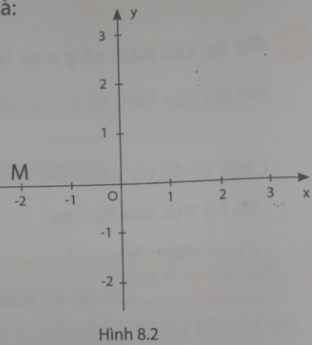
A. M(-2; 0)
B. M(0; 2)
C. M(0; -2)
D. M(2; 0)
Hướng dẫn:
M(-2; 0). Chọn A

Bình luận