Giải phát triển năng lực toán 7 bài 2: Hai tam giác bằng nhau
Giải bài 2: Hai tam giác bằng nhau - Sách phát triển năng lực trong môn toán 7 tập 1 trang 114. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. LÝ THUYẾT
1. Sử dụng kéo, giấy màu có ô vuông và thước thẳng để thực hiện theo các bước sau:
Bước 1: Trên mảnh giấy có ô vuông, vẽ hai tam giác như hình 2.1.
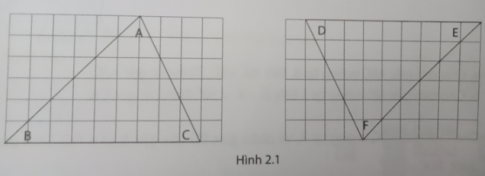
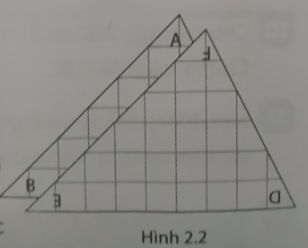
Bước 2: Cắt mảnh giấy để được các hình tam giác. Đặt các hình tam giác chồng khít lên nhau (h 2.2). Khi đó, hai tam giác ABC và DEF được gọi là hai tam giác bằng nhau.
a. Xác định tất cả các cặp góc và các cặp cạnh chồng khít lên nhau.
b. Nhận xét về mối quan hệ giữa các cặp góc và các cặp cạnh đó.
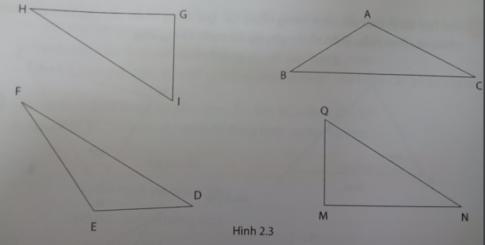
2. Quan sát các tam giác trong hình 2.3 rồi dùng thước chia khoảng và thước đo góc để chỉ ra các tam giác có các cạnh và các góc bằng nhau rồi điền vào bảng bên dưới.
| Tam giác bằng nhau | Cặp cạnh bằng nhau | Cặp góc bằng nhau |
| EFD và ACB | EF = AC | $\widehat{A}=\widehat{E}$ |
| GHI và MNQ | GI = QM | $\widehat{G}=\widehat{M}$ |
Hướng dẫn:
| Tam giác bằng nhau | Cặp cạnh bằng nhau | Cặp góc bằng nhau |
| EFD và ACB | EF = AC; ED = AB; DF = BC | $\widehat{A}=\widehat{E}$; $\widehat{F}=\widehat{C}$; $\widehat{B}=\widehat{D}$ |
| GHI và MNQ | GI = QM; GH = MN; HI = QN | $\widehat{G}=\widehat{M}$; $\widehat{N}=\widehat{H}$; $\widehat{Q}=\widehat{I}$ |
3. Điền vào chỗ chấm để hoàn thành bảng sau:
Nếu hai tam giác ABC và A'B'C' có AB = A'B'; BC = B'C'; CA = C'A' và $\widehat{A}=\widehat{A'}$; $\widehat{B}=\widehat{B'}$; $\widehat{C}=\widehat{C'}$ thì hai tam giác ABC và A'B'C'
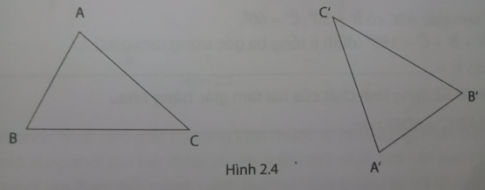
Hai đỉnh A và A' , B và B' , C và C' gọi là .................................
Hai góc ....................................................... gọi là hai góc tương ứng.
Hai cạnh bằng nhau gọi là hai cạnh ....................................
Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng ......................, các ..................... bằng nhau.
Kí hiệu: ....................... đọc là tam giác ABC bằng tam giác A'B'C'.
$\Delta ABC = \Delta A'B'C'$ nếu $\left\{\begin{matrix}.............\\ .............\end{matrix}\right.$
Hướng dẫn:
Hai đỉnh A và A' , B và B' , C và C' gọi là hai đỉnh tương ứng.
Hai góc $\widehat{A}$ và $\widehat{A'}$; $\widehat{B}$ và $\widehat{B'}$; $\widehat{C}$ và $\widehat{C'}$ gọi là hai góc tương ứng.
Hai cạnh bằng nhau gọi là hai cạnh tương ứng.
Định nghĩa: Hai tam giác bằng nhau là hai tam giác có các cạnh tương ứng bằng nhau, các góc tương ứng bằng nhau.
Kí hiệu: $\Delta ABC = \Delta A'B'C'$ đọc là tam giác ABC bằng tam giác A'B'C'.
$\Delta ABC = \Delta A'B'C'$ nếu $\left\{\begin{matrix}AB = A'B'; AC = A'C'; BC = B'C'\\ \widehat{A}= \widehat{A'}; \widehat{B} = \widehat{B'}; \widehat{C} = \widehat{C'}\end{matrix}\right.$
4. Em hãy đánh dấu các cạnh bằng nhau, các góc bằng nhau của cặp tam giác bằng nhau sau theo mẫu. Điền số góc, độ dài cạnh tương ứng.
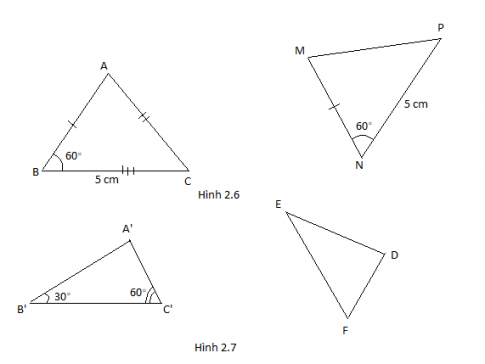
Hướng dẫn:
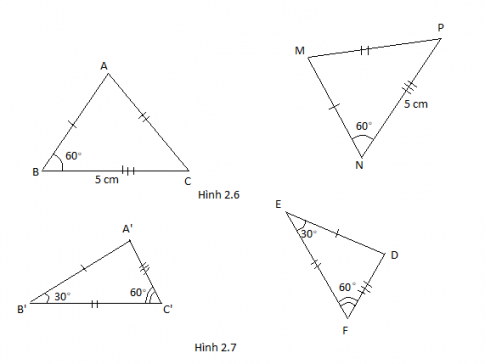
5. Ở hoạt động 4, em hãy tìm góc D mà không sử dụng thước đo góc theo các bước sau:
Bước 1: Sử dụng tính chất của tổng ba góc trong một tam giác
Xét tam giác A'B'C' có $\widehat{B'} = 30^{\circ}$; $\widehat{C'} = 60^{\circ}$ và $\widehat{A'} + \widehat{B'} + \widehat{C'}=180^{\circ}$ (định lí tổng ba góc trong một tam giác)
Do đó $\widehat{A'}$ = .........................................................................................................
Bước 2: Sử dụng tính chất của hai tam giác bằng nhau
$\Delta A'B'C' = \Delta DEF$ nên .......................................................................................
Hướng dẫn:
Bước 1: Sử dụng tính chất của tổng ba góc trong một tam giác
Xét tam giác A'B'C' có $\widehat{B'} = 30^{\circ}$; $\widehat{C'} = 60^{\circ}$ và $\widehat{A'} + \widehat{B'} + \widehat{C'}=180^{\circ}$ (định lí tổng ba góc trong một tam giác)
Do đó $\widehat{A'} = 180^{\circ}-30^{\circ}-60^{\circ}=90^{\circ}$
Bước 2: Sử dụng tính chất của hai tam giác bằng nhau
$\Delta A'B'C' = \Delta DEF$ nên $\widehat{EDF}=\widehat{B'A'C'}=90^{\circ}$.

Bình luận