Giải phát triển năng lực toán 7 bài 1: Tập hợp Q các số hữu tỉ
Giải bài 1: Tập hợp Q các số hữu tỉ - Sách phát triển năng lực trong môn toán 7 tập 1 trang 7. Phần dưới sẽ hướng dẫn trả lời và giải đáp các câu hỏi trong bài học. Cách làm chi tiết, dễ hiểu, Hi vọng các em học sinh nắm tốt kiến thức bài học.
A. Lý thuyết
1. Số hữu tỉ
a. Viết các số sau dưới dạng phân số:
5 = ..............; -3 = ................; 1,5 = ..............;
0 = ..............; $2\frac{1}{3}$ = .................
Nhận xét: Các số trên được gọi là số hữu tỉ
Số hữu tỉ là số viết được dưới dạng phân số $\frac{a}{b}$, trong đó a, b $\in $ Z, b $\neq $ 0.
Tập hợp các số hữu tỉ được kí hiệu là Q
b. Điền kí hiệu ($\in , \notin ,\subset $) thích hợp vào chỗ trống:
-5 ... Z -5 ... Q $\frac{-3}{5}$ ... Z
$\frac{-3}{5}$ ... Q N ... Z ... Q
c. Quan sát sơ đồ Ven sau, điền tên các tập hợp vào ô trống:
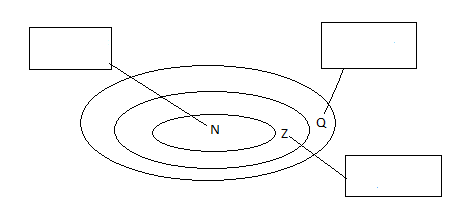
Hãy thảo luận theo nhóm và thực hiện các yêu cầu sau:
- Tìm mối quan hệ giữa các tập N, Z, Q.
- Cho tập hợp C = ${-2; 1; \frac{-3}{5}; \frac{6}{3}; 0,25; 7; \frac{3}{-4}}$. Viết các tập hợp sau:
Tập hợp A gồm các phần tử của C thuộc tập hợp Z mà không thuộc tập hợp N.
Tập hợp B gồm các phần từ của C thuộc tập hợp Q mà không thuộc tập hợp Z.
Hướng dẫn:
a. $5=\frac{5}{1}$; $-3 = \frac{-6}{2}$; $1,5 = \frac{3}{2}$;
$0 = \frac{0}{3}$; $2\frac{1}{3}=\frac{7}{3}$
b. -5 $\in $ Z -5 $\in $ Q $\frac{-3}{5}$ $\notin$ Z
$\frac{-3}{5}$ $\in $ Q N $\subset $ Z $\subset $ Q
c.

- Mối quan hệ giữa các tập N, Z, Q: N thuộc Z thuộc Q
- Tập A = {-2}
- Tập B = {$\frac{-3}{5}; \frac{6}{3}; 0,25; \frac{3}{-4}$}
2. Biểu diễn số hữu tỉ trên trục số
a. Tương tự như số nguyên, ta có thể biểu diễn mọi số hữu tỉ trên trục số.
Để biểu diễn số hữu tỉ $\frac{4}{-6}$ trên trục số ta làm như sau:
Bước 1: Viết $\frac{4}{-6}$ dưới dạng phân số tối giản có mẫu số dương $\frac{4}{-6} = \frac{-2}{3}$;
Bước 2: Chia đoạn thẳng đơn vị (từ -1 đến 0) thành 3 phần bằng nhau (ứng với mẫu của phân số là 3), mỗi phần là một đơn vị mới.
Bước 3: Lấy từ điểm 0, về phía bên trái 2 đơn vị mới (ứng với tử của phân số là -2) ta được điểm biểu diễn số hữu tỉ $\frac{-2}{3}$ hay $\frac{4}{-6}$
b. Bằng cách tương tự, em hãy biểu diễn các số hữu tỉ sau trên trục số:
-0,25 
$\frac{8}{3}$ ![]()
Hướng dẫn:
+) -0,25
Bước 1: Ta viết -0,25 dưới dạng phân số tối giản có mẫu dương -0,25 = $\frac{-1}{4}$
Bước 2: Chia đoạn thẳng đơn vị từ -1 đến 0 thành 4 phần bằng nhau (ứng với mẫu của phân số là 4), mỗi phần là một đơn vị mới.
Bước 3: Lấy từ điểm 0, về phía bên trái 1 đơn vị mới (ứng với tử của phân số là -1) ta được điểm biểu diễn số hữu tỉ $\frac{-1}{4}$ hay -0,25.
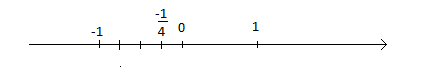
+) $\frac{8}{3}$
Bước 1: Ta thấy $\frac{8}{3}$ là phân số tối giản với mẫu số dương.
Bước 2: Chia các đoạn thẳng đơn vị (từ 0 đến 1, 1 đến 2, 2 đến 3) thành 3 phần bằng nhau (ứng với mẫu của phân số là 3), mỗi phần là một đơn vị mới.
Bước 3: Lấy từ điểm 2, về phía bên phải 2 đơn vị mới (ứng với tử của phân số là 8) ta được điểm biểu diễn số hữu tỉ $\frac{8}{3}$.

3. So sánh hai số hữu tỉ
a. Điền số hoặc dấu (>, = , <) thích hợp vào chỗ trống:
So sánh -0,25 và $\frac{1}{-2}$
Ta có: -0,25 = $\frac{-1}{...}$ ; $\frac{1}{-2}$ = $\frac{...}{4}$
Vì: -1 > -2 và 4 > 0 nên $\frac{-1}{...}$ > $\frac{...}{4}$ hay -0,25 ... $\frac{1}{-2}$
Nhận xét: Ta có thể so sánh hai số hữu tỉ bằng cách viết chúng dưới dạng phân số có mẫu dương rồi so sánh hai phân số đó.
b. Em hãy sắp xếp lại thứ tự các câu ở cột A sang cột B để được một cách so sánh hai số hữu tỉ:
| Cột A | Cột B |
| So sánh các tử số | Bước 1: ................................... |
| Quy đồng mẫu số các phân số | Bước 2: ................................... |
| Viết các phân số hữu tỉ x và y dưới dạng phân số có mẫu số dương | Bước 3: ................................... |
c. So sánh các số hữu tỉ sau:
$\frac{-2}{3}$ và 0 $\frac{4}{5}$ và 0 $\frac{3}{-5}$ và $\frac{-7}{9}$
* Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương. Số hữu tỉ nhỏ hơn 0 là số hữu tỉ âm. Số 0 là một số hữu tỉ, nhưng không là số hữu tỉ dương và cũng không là số hữu tỉ âm.
Hướng dẫn:
a. Ta có: -0,25 = $\frac{-1}{4}$ ; $\frac{1}{-2}$ = $\frac{-2}{4}$
Vì: -1 > -2 và 4 > 0 nên $\frac{-1}{4}$ > $\frac{-2}{4}$ hay -0,25 > $\frac{1}{-2}$
b.
| Cột A | Cột B |
| So sánh các tử số | Bước 1: Viết các phân số hữu tỉ x và y dưới dạng phân số có mẫu số dương |
| Quy đồng mẫu số các phân số | Bước 2: Quy đồng mẫu số các phân số |
| Viết các phân số hữu tỉ x và y dưới dạng phân số có mẫu số dương | Bước 3: So sánh các tử số |
c.
+) $\frac{-2}{3}$ và 0
Ta có: 0 = $\frac{0}{3}$
Vì: -2 < 0 và 3 > 0 nên $\frac{-2}{3}$ < 0
+) $\frac{4}{5}$ và 0
Ta có: 0 = $\frac{0}{5}$
Vì: 4 > 0 và 5 > 0 nên $\frac{4}{5}$ > 0
+) $\frac{3}{-5}$ và $\frac{-7}{9}$
Ta có: $\frac{3}{-5}$ = $\frac{-27}{45}$ = $\frac{-35}{45}$
Vì: -27 > -35 và 5 > 0 nên $\frac{3}{-5}$ > $\frac{-7}{9}$



Bình luận