Giải câu 5 trang 103 sách phát triển năng lực toán 7 tập 1
5. Cho góc xOy, lấy điểm A trên tia Ox, từ A kẻ đường thẳng a vuông góc với tia Ox, lấy điểm B trên tia Oy, qua điểm B kẻ đường thẳng b vuông góc với tia Oy.
a. Nếu $\widehat{xOy} < 180^{\circ}$ thì hai đường thẳng a, b có cắt nhau không? Vì sao?
b. Nếu $\widehat{xOy} = 180^{\circ}$ thì hai đường thẳng a, b có cắt nhau không? Vì sao?
c. Giả sử $\widehat{xOy} = 90^{\circ}$, hãy chứng minh a $\perp $ b.
a.
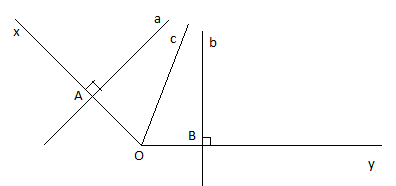
Giả sử a và b song song.
Từ O kẻ đường thẳng c sao cho c // a. Suy ra c // b. (hình vẽ)
Ta có: a // c nên $\widehat{xAa} = \widehat{AOc} = 90^{\circ}$ (hai góc đồng vị)
b // c nên $\widehat{cOB} = \widehat{bBy} = 90^{\circ}$ (hai góc đồng vị)
Do đó $\widehat{xOy} = \widehat{AOc} + \widehat{cOB} = 90^{\circ} + 90^{\circ} = 180^{\circ}$ (trái với giả thiết bài toán $\widehat{xOy} < 180^{\circ}$)
Vậy a và b không song song. Hay a và b cắt nhau.
b.
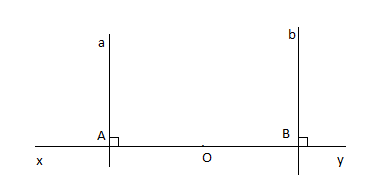
$\widehat{xOy} = 180^{\circ}$ và A thuộc Ox, B thuộc Oy nên A, O, B thẳng hàng hay đường thẳng xy đi qua 3 điểm A, O, B
Ta có a $\perp $ xy tại A và b $\perp $ xy tại B nên a // b.
Do đó hai đường thẳng a và b không cắt nhau.
c.

Ta thấy: a $\perp $ Ox và Oy $\perp $ Ox nên a // Oy (1)
Mà b $\perp $ Oy (2)
Từ (1) và (2) suy ra a $\perp $ b

Bình luận