Giải câu 49 bài: Luyện tập sgk Toán 8 tập 1 Trang 93
Câu 49 : Trang 93 sgk toán 8 tập 1
Cho hình bình hành ABCD. Gọi I, K theo thứ tự là trung điểm của CD, AB. Đường chéo BD cắt AI, CK theo thứ tự ở M và N. Chứng minh rằng:
a) AI // CK
b) DM = MN = NB
Theo giả thiết ta có hình vẽ sau:
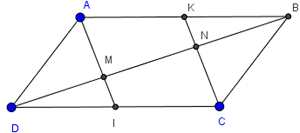
a) Do ABCD là hình bình hành, mà I, K lần lượt là trung điểm của AB và DC
=> AK = KB = DI = DC
Mà AK // IC (do AB // DC)
=>Tứ giác AICK có AK // IC, AK = IC nên là hình bình hành.
Do đó AI // CK (Đpcm)
b) Xét ∆DCN có DI = IC và IM // CN.
=>MI là đường trung bình của ∆DCN
=>M là trung điểm của DN =>DM = MN
Chứng minh tương tự đối với ∆ABM ta có MN = NB.
Vậy DM = MN = NB (đpcm)
Từ khóa tìm kiếm Google: giải câu 49 trang 93 sgk Toán 8 tập 1, giải bài tập 49 trang 93 Toán 8 tập 1, câu 49 trang 93, Câu 49 bài 7: Hình bình hành - sgk Toan 8 tập 1

Bình luận