• Ôn tập lý thuyết
• Hướng dẫn giải bài tập sgk

A. LÝ THUYẾT

1. Phép chia hết

Ví dụ: Thực hiện phép chia (2x⁴ – 13x³ – 15x² + 11x – 3)  chia cho (x² – 4x – 3) 

• Đặt phép chia
• Chia hạng tử bậc cao nhất của đa thực bị chia cho hạng tử bậc cao nhất của đa thức chia.
• Nhân kết quả vừa thu được với đa thức chia, rồi lấy đa thức bị chia trừ đi tích nhận được.
• Chia hạng tử bậc cao nhất của dư thứ nhất cho hạng tử bậc cao nhất của đa thức chia.
• Thực hiện tương tự ta được

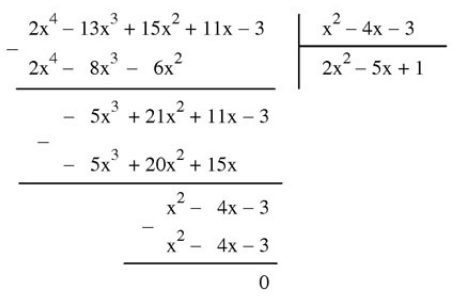
2. Phép chia có dư

Người ta chứng minh được rằng, với hai đa thức A và B của một biến, B ≠ 0 tồn tại duy nhất hai đa thức Q và R sao cho:

A = B . Q + R, với R = 0 hoặc bậc bé hơn bậc của 1

• Nếu R = 0, ta được phép chia hết.
• Nếu R ≠ 0, ta được phép chia có dư.