Giải câu 47 bài: Luyện tập sgk Toán 8 tập 1 Trang 93

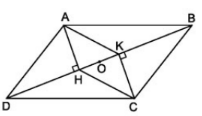
a) Xét tam giác vuông AHD và tam giác vuông CKD có:

           AD = CB (do ABCD là hình bình hành)

          $\widehat{ADH} = \widehat{DBC}$ (AD // BC => hai so le trong)

=>  ∆AHD =  ∆CKB (cạnh huyền, góc nhọn)

=> AH = CK (hai cạnh tương ứng) (1)

Xét tứ giác AHCK có

AH vuông góc với DB

CK vuông góc với DB.

=>Nên AH // CK (2)

Từ (1) và (2) => AHCK là hình bình hành (đpcm)

b) Xét hình bình hành AHCK có:

O là trung điểm của HK

Mặt khác, tứ giác AHCK là hình bình hành

=> AC giao với HK tại O => ba điểm A, O, C thẳng hàng.