Bài tập về vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình vuông

1. 

Tứ giác KHED là hình vuông.

Vì $\Delta $BDK vuông có $\widehat{B}=45^{\circ}$ nên là tam giác vuông cân, do đó BD = DK 

Chứng minh tương tự, HE = EC.

Vì BD = DE = EC theo giả thiết nên KD = DE = EH

Tứ giác KHED có KD // HE, KD = HE nên là hình bình hành.

Hình bình hành này có $\widehat{D}=90^{\circ}$ nên nó là hình chữ nhật.

Mà hình chữ nhật KHED có KD = DE nên nó là hình vuông.

2.

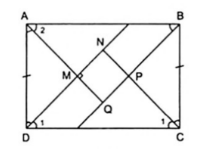
Vì $\Delta $NCD có $\widehat{C_{1}}=\widehat{D_{1}}=45^{\circ}$ nên vuông cân tại N.

Suy ra $\widehat{N}=90^{\circ}$ và ND = NC (1)

Chứng minh tương tự, $\widehat{P}=\widehat{Q}=90^{\circ}$. Tứ giác MNPQ có ba góc vuông nên là hình chữ nhật.

$\Delta $AMD = $\Delta $BPC (g-c-g) $\Rightarrow $ MD = PC (2)

Trừ theo vế đẳng thức (1) cho đẳng thức (2) ta được NM = NP

Như vậy hình chữ nhật MNPQ có hai cạnh kề bằng nhau nên là hình vuông.

3.

Ta cần chứng minh 4 tam giác vuông EFG, IHG, CBI, CDE bằng nhau.

FG = GH = BI = DE

EF = HI = BC = CD

$\Rightarrow $ EG = GI = IC = CE và $\widehat{ICB}=\widehat{DCE}$

$\widehat{DCE}+\widehat{ECB}=90^{\circ}$

$\Rightarrow \widehat{ICB}+\widehat{ECB}=90^{\circ}=\widehat{ECI}$

$\Rightarrow $ tứ giác EGIC là hình vuông.