Bài tập về vận dụng dấu hiệu nhận biết để chứng minh một tứ giác là hình thoi

1.

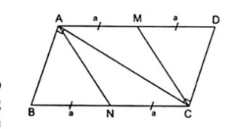
Áp dụng định nghĩa và giả thiết vào hình bình hành ABCD ta được:

AB // CD

AC $\perp $ CD

$\Rightarrow AB \perp AC$. Do đó $\Delta $ABC vuông ở A, $\Delta $ACD vuông ở C.

Do M, N là trung điểm của AD, BC theo giả thiết nên AN, CM thứ tự là trung tuyến ứng với cạnh huyền của hai tam giác vuông ABC và ACD

Do đó AN = $\frac{1}{2}$BC; CM = $\frac{1}{2}$AD

Mà AD = BC; AM = MD; BN = NC

$\Rightarrow $ AM = MC = CN = NA

Tứ giác AMCN có bốn cạnh bằng nhau nên là hình thoi.

2.

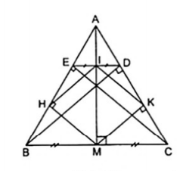
Xét $\Delta $BDC và $\Delta $CEB là 2 tam giác vuông có:

chung BC

$\widehat{DCB}=\widehat{EBC}$ ($\Delta $ABC cân tại A)

$\Rightarrow $ $\Delta $BDC = $\Delta $CEB

$\Rightarrow $ EB = DC (1)

Dễ thấy ED // BC nên tứ giác DEBC là hình thang. (2)

Từ (1), (2) ta được tứ giác DEBC là hình thang cân.

Có: MK $\perp $ AC; BD $\perp $ AC nên MK // BD.

$\Delta $BDC có M là trung điểm của BC; MK // BD nên MK là đường trung bình của $\Delta $BDC

$\Rightarrow $ K là trung điểm của DC và MK = $\frac{1}{2}$DB

Ta lần lượt chứng minh MH, HI, IK cũng là đường trung bình của các tam giác $\Delta $BEC, $\Delta $BED, $\Delta $EDC

$\Rightarrow $ HM = $\frac{1}{2}$EC; HI = $\frac{1}{2}$BD; IK = $\frac{1}{2}$EC.

Mà EC = BD (do DEBC là hình thang cân)

$\Rightarrow $ HI = IK = KM = MH

Vậy tứ giác HUKM là hình thoi.

3.

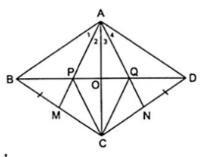
Tứ giác APCQ là hình thoi.

Giải thích:

$\Delta $ABM = $\Delta $ADN (c.g.c)

$\Rightarrow \widehat{A_{1}}=\widehat{A_{4}}$, do đó $\widehat{A_{2}}=\widehat{A_{3}}$.

Gọi O là giao điểm của AC và BD thì AC $\perp $ BD

$\Delta $APQ có đường cao AO là đường phân giác nên OP = OQ

Tứ giác APCQ có OP = OQ; OA = OC và AO là tia phân giác của $\widehat{PAQ}$ nên tứ giác APCQ là hình thoi.