Bài tập về sử dụng định nghĩa và tính chất của hình thoi để tính toán, chứng minh các đoạn thẳng bằng nhau, các góc bằng nhau, các đường thẳng vuông góc với nhau
1. Hình thoi ABCD có chu vi bằng 16cm, đường cao AH = 2cm. Tính các góc của hình thoi.
2. Hình thoi ABCD có $\widehat{A}=60^{\circ}$, kẻ hai đường cao BE và BF. Tam giác BEF là tam giác gì? Vì sao?
3. Cho hình bình hành ABCD có AD = 2AB. Gọi E là chân đường vuông góc kẻ từ C đến đường thẳng AB, M là trung điểm của AD, F là chân đường vuông góc kẻ từ M đến CE và MF cắt BC ở N.
a) Tứ giác MNCD là hình gì? Vì sao?
b) Tam giác EMC là tam giác gì? Vì sao?
c) Chứng minh rằng $\widehat{BAD}=2\widehat{AEM}$
1.
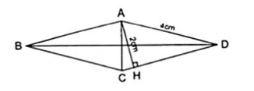
Vì hình thoi có chu vi bằng 16cm nên cạnh AD = 4cm.
Lại có đường cao AH = 2cm.
$\Delta $AHD vuông tại H có AD = 2AH nên $\widehat{ADH}=30^{\circ}$
Do đó $\widehat{B}=\widehat{D}=30^{\circ}$; $\widehat{A}=\widehat{C}=150^{\circ}$
2.
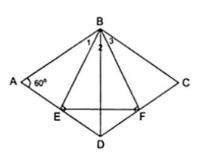
Ta có $\Delta $ABE = $\Delta $BCF (cạnh huyền - góc nhọn)
$\Rightarrow $ BE = BF (1)
$\Rightarrow $ $\Delta $BEF cân.
$\Delta $ABE và $\Delta $BFC là các tam giác vuông có $\widehat{BAE}=\widehat{BCF}=60^{\circ}$
$\Rightarrow \widehat{ABE}=\widehat{CBF}=30^{\circ}$
Mà $\widehat{ABC}=120^{\circ} \Rightarrow \widehat{EBF}=60^{\circ}$ (2)
Từ (1) và (2) suy ra $\Delta $BEF đều.
3.

a) Tứ giác MNCD là hình thoi vì có 4 cạnh bằng nhau.
b) $\Delta $MCE là tam giác cân tại M vì có MF vừa là đường cao vừa là đường phân giác.
c) Đặt $\widehat{E_{1}}=a$ thì $\widehat{M_{1}}=a$ vì so le trong với $\widehat{E_{1}}$.
$\widehat{M_{2}}=\widehat{M_{1}}=a$ vì $\Delta $MEC cân tại M có MF là phân giác.
Lại có $\widehat{M_{2}}=\widehat{M_{3}}=a$ theo tính chất hình thoi.
Do đó $\widehat{BAD}=\widehat{NMD}=2a=2\widehat{AEM}$

Bình luận