Bài tập về chứng minh hai tam giác đồng dạng

1.

a) Ta có:

$\frac{40}{8}=\frac{50}{10}=\frac{60}{12}=5$

Do đó hai tam giác mà các cạnh có độ dài 4cm; 5cm; 6cm và 8mm; 10mm; 12mm đồng dạng với nhau.

b) Ta có:

$\frac{3}{9}=\frac{4}{12}=\frac{5}{15}=\frac{1}{3}$

Do đó hai tam giác mà các cạnh có độ dài 3cm; 4cm; 6cm và 9cm; 15cm; 18cm đồng dạng với nhau.

c) Ta có:

$\frac{1}{0,5}=\frac{2}{1}=\frac{2}{1}=2$

Do đó hai tam giác mà các cạnh có độ dài 1dm; 2dm; 2dm và 1dm; 1dm; 0,5dm đồng dạng với nhau.

2.

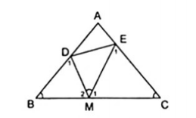
Ta có: 

$\widehat{BME}=\widehat{BMD}+\widehat{DME}=\widehat{BMD}+a$

$\widehat{BME}=\widehat{MEC}+\widehat{ECM}=\widehat{MEC}+a$ ($\widehat{BME}$ là góc ngoài $\Delta $MEC)

$\Rightarrow \widehat{BMD}=\widehat{MEC}$

Xét $\Delta $MBD và $\Delta $ECM có:

$\widehat{BMD}=\widehat{MEC}$

$\widehat{MBD}=\widehat{MCE}$

$\Rightarrow \Delta MBD \sim  \Delta ECM$ (g-g)

3.

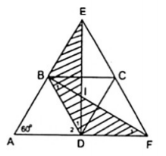
a) Áp dụng định lí Ta-lét vào $\Delta $EAF có: BC // AF và DC // AE, ta được:

$\frac{EB}{BA}=\frac{EC}{CF}$

$\frac{FD}{DA}=\frac{EC}{CF}$

$\Rightarrow \frac{EB}{BA}=\frac{AD}{DF}$

b) Vì ABCD là hình thoi có $\widehat{A}=60^{\circ}$ nên các $\Delta $ABD và $\Delta $BCD là các tam giác đều.

Do đó AB = BD = DA

Từ câu a suy ra $\frac{EB}{ED}=\frac{BD}{BF}$

Ta lại có $\widehat{EBD}=\widehat{BDF}=120^{\circ}$

Vậy $\Delta EBD\sim \Delta BDF$

4. 

Từ giả thiết ta có:

$\frac{AB}{BH}=\frac{20}{12}=\frac{5}{3}$

$\frac{AC}{AH}=\frac{5}{3}$

$\Rightarrow \frac{AB}{BH}=\frac{AC}{AH}$

Xét $\Delta $ABH và $\Delta $AHC là 2 tam giác vuông tại H có:

$\frac{AB}{BH}=\frac{AC}{AH}$

$\Rightarrow \Delta ABH\sim \Delta CAH$ (cạnh huyền-cạnh góc vuông)

5.

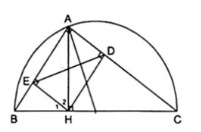
Từ giả thiết ta có tứ giác ADHE là hình chữ nhật vì có ba góc vuông nên $\Delta ADE=\Delta HEA$ 

$\Rightarrow \Delta ADE\sim \Delta HEA$ (1)

Lại có: 

$\widehat{B}+\widehat{H_{1}}=90^{\circ}$

$\widehat{H_{1}}+\widehat{H_{2}}=90^{\circ}$

$\Rightarrow \widehat{B}=\widehat{H_{2}}$

$\Rightarrow \Delta BAC\sim \Delta HEA$ (g-g) (2)

Từ (1), (2) ta được $\Delta ADE\sim \Delta BAC$